Детерминированные методы расчета элементов и узлов

Статический режим. Целью анализа является исследование статических и переходных режимов ММС, расчет коэффициентов чувствительности динамических и статических параметров, статистический анализ. При этом режимы работы определяются численными методами одновариантного анализа, а чувствительность требует использования многовариантного анализа.

Расчет статического режима ММС заключается в решении нелинейных, в общем случае трансцендентных уравнений, т.е. в определении стационарной точки решения системы

F(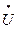,U,t) (2.21)

при постоянных уровнях возбуждения.

В данном разделе рассматриваются численные методы решения системы (2.21), которые позволяют получить приближенное решение 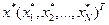, такое что 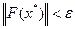.где 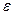— заданная точность расчета.

Существуют два основных подхода к расчету статического режима.

Первый подход основан на представлении статического режима как предельного, к которому стремятся переходные процессы в схеме при 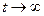. При этом используются методы интегрирования системы дифференциальных уравнений (2.21) при постоянных уров­нях входных сигналов в течение модельного времени T₀, достаточного для затухания переходных процессов.

Второй подход основан на итерационных методах решения нелинейных уравнений. Наиболее распространенными итерационными методами решения нелинейных уравнений являются методы Ньютона, Бройдена, изменения параметров [17].

Итерационная формула Ньютона-Рафсона

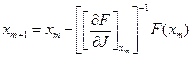, здесь 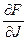- матрица Якоби.

Итерационная формула Бройдена

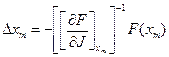, , где 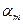- скалярный коэффициент.

Для решения систем линейных алгебраических уравнений применяются методы Гаусса, Краута, LU - разложения [18, 19].

Переходные процессы. Для оценки быстродействия схем необходимо проводить анализ переходных процессов. Анализ переходных процессов заключается в численном интегрировании системы нелинейных обыкновенных дифференциальных уравнений (ОДУ), описывающих физические процессы, протекающие в схемах.

Формулы численного решения ОДУ представляют собой аппроксимирующие выражения, связывающие 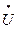и U. Формула называется явной, если

,

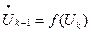и неявной, если

.

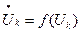В формулах (2.22) и (2.23) кроме U_k могут фигурировать и некоторые другие величины. Если в формулах присутствуют члены с производными U no t порядка выше первого или результаты дополнительных вычислений на данном шаге, то метод решения ОДУ называется одношаговым. К одношаговым методам относятся методы разложения в ряд Тейлора и Рунге — Кутты.

В формулах многошаговых методов присутствуют значения U и 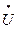, вычисленные на предыдущих шагах интегрирования.

Из числа явных методов в основном применяются:

метод Рунге — Кутты

;

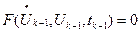F( B ,U_k-1+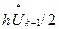,t_k-1+h/2)=0;

F( C ,U_k-1+h B /2,t_k-1+h/2)=0;

F( D ,U_k-1+h C,t_k-1+h)=0;

U_k =U_k-1+h(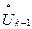+2 B +2 C + D )/6,

где h - шаг интегрирования, U_k-1,В,С,D,U _k - векторы;

неявный метод Рунге - Кутты четвертого порядка

F(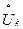, U_k, t_k)=0;

F( B, U_k - 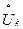h/2, t_k-h/2)=0;

F( C, U_k – B h/2, t_k – h/2)=0;

F( D, U_k – C h, t_k)=0;

U_k =U_k-1+h(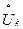+2 B +2 C + D )/6;

метод Адамса — Башфорта

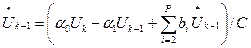
Из неявных методов наибольшее применение получили:

метод Адамса — Маултона

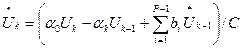
метод Гира

.

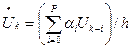Анализ чувствительности. Задача определения коэффициентов чувствительности выходных параметров схемы к изменению ее входных параметров позволяет определить степень влияния разброса параметров компонентов схемы на ее выходные параметры и необходима при оптимизации ММС.

Задача детерминированной оптимизации электронных схем сводится к задаче поиска экстремума критерия оптимизации, который определяется как функция выходных параметров Ф = Ф[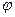(Р)], где 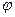= (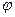₁ …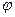_M)^T — вектор-столбец выходных параметров схемы; Р = (Р₁...Р_m) — вектор-строка входных параметров схемы; Ф — критерий оптимизации; М и m — соответственно число выходных и входных параметров.

Обычно известна аналитическая зависимость критерия оптимизации (см. гл. 1) от выходных параметров схемы. Поэтому градиент функции может быть записан в виде

.

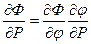Компоненты вектора 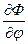вычисляются по аналитическим зависимостям как функции выходных параметров.

Для вычисления коэффициентов чувствительности используются:

Метод приращений. По этому методу коэффициент чувствительности статического j -го выходного параметра к изменению i- го входного параметра определяется по формуле

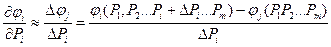
Метод присоединенной схемы. В основе метода лежит теорема Теллегена, утверждающая, что алгебраическая сумма произведений токов и напряжений всех ветвей равна нулю:

,

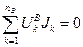где , J_k - напряжение и ток k -й ветви, п _в — число ветвей схемы.

Метод дифференцирования уравнений. Суть метода состоит в следующем. Если U* — решение J(U, E, Р) = 0, то справедлива следующая система тождеств J(U*, Е, Р) = 0

Продифференцировав U* по параметрам P, получим

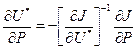и .

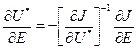Вариационный метод. Основан на использовании вариационного исчисления для получения выражения векторной чувствительности скалярного функционала качества относительно входных параметров. Градиент функционала качества рассчитывается по формуле

,

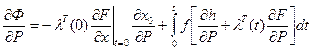где значения 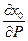вычисляются из условия трансверсальности для начального состояния; х — вектор переменных состояния; h — известная функция переменных х, Р, t.

Макромоделирование элементов и устройств ЭВМ. Макромодель цифровой схемы — это математическая модель схемы, воспроизводящая логические, статические и динамические характеристики исследуемой схемы.

Основной целью перехода к макромодели является упрощение исходной схемы, что приводит к уменьшению порядка системы алгебродифференциальных уравнений, описывающих общую анализируемую схему, но понижает точность моделирования.

Естественно, что упрощение модели приводит к сужению области применения разработанной модели. Однако при этом можно весьма просто в модель вводить зависимость статических и динамических параметров от внешних и внутренних воздействий. Применение макромоделей позволяет широко использовать методику поэтапного проектирования, объединяющего этапы логического и функционального проектирований. При этом устройство может моделироваться как на компонентном уровне, так и на функциональных макромоделях. Выделяют три основных уровня макромоделей [19]: первый, второй, третий.

Макромодели первого уровня образуют простейшие макромодели, отображающие только функционально-логическое назначение моделируемого узла без учета его схемотехнических и технологических особенностей. При этом различают три способа упрощения: использование более простых моделей компонентов; упрощение схем посредством замены части ее узлов их простейшими реализациями в виде зависимых источников напряжений и токов; исключение отдельных компонентов, слабо влияющих на выходные характеристики. Данный уровень макромодели оказывается достаточным для параметрической оптимизации логических и триггерных схем.

Суть подхода к построению макромодели первого уровня состоит в последовательном упрощении структуры и составлении упрощенных уравнений, описывающих статические и динамические характеристики.

Макромодель второго уровня основана на формальной аппроксимации внешних характеристик схем. Схемные элементы таких ММС обычно не имеют сходства с принципиальной схемой и инвариантны к различным элементным базисам.

Макромодель второго уровня состоит из блоков: входного, реализующего логические и динамические входные характеристики; промежуточного, обеспечивающего заданные динамические и статические характеристики; выходного, воспроизводящего выходную характеристику и задержку схемы.

Макромодель третьего уровня использует программы, совмещающие схемотехническое и регистровое моделирование [20].

[V1]