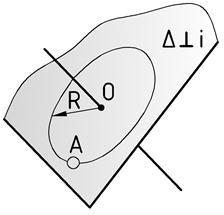
В процессе вращения геометрической фигуры каждая ее точка описывает в пространстве окружность, плоскость которой перпендикулярна к оси вращения, а центр – в точке пересечения оси и этой плоскости (Рис.55). Если ось вращения – проецирующая прямая и, соответственно, плоскость вращения – плоскость уровня, то следует вывод:
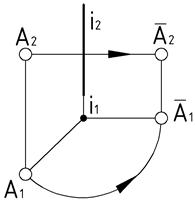
Траектория вращения точки на плоскость, перпендикулярную к оси вращения, проецируется без искажения, а на плоскость, параллельную оси, – в виде прямой линии, параллельной оси проекций (Рис.56).
|
| Рис.55 |
|
| Рис.56 |
Способ может быть использован для всех 4-х задач преобразования.
|
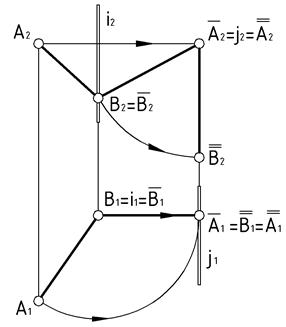
| Рис.57 |
Пример (Рис.57). Спроецировать отрезок 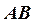 в натуральную величину и – в точку. Для первого вращения использовать заданную ось
в натуральную величину и – в точку. Для первого вращения использовать заданную ось 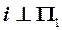 . Для второго вращения ось j задать самостоятельно.
. Для второго вращения ось j задать самостоятельно.
Решение:
1) Повернуть отрезок 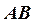 вокруг оси i до положения фронтали
вокруг оси i до положения фронтали 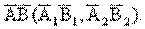
2) Через один из концов отрезка задать ось вращения 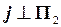 и повернуть отрезок
и повернуть отрезок 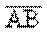 в положение горизонтально проецирующей прямой
в положение горизонтально проецирующей прямой 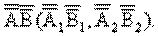
 2014-02-02
2014-02-02 570
570








