Задача о распределении бюджета
Пусть требуется принять решение о выделении средств для нескольких вариантов капиталовложений с целью максимизации прибыли. Имеются прогнозные данные аналитического отдела, представленные в таблице.
| Вариант | Чистая прибыль, тыс. д.е. | Вложения по годам, тыс. д.е. | ||||
| Расширение завода в стране А | ||||||
| Расширение мощностей по производству ПК в своей стране | ||||||
| Открытие нового завода в стране Б | ||||||
| Расширение мощностей по производству комплектующих в своей стране | ||||||
| Имеющиеся средства |
Данная задача является характерным примером двоичной модели ЦЛП. Пусть 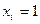 , если проект
, если проект 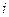 принимается, и
принимается, и 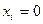 в противном случае. При этих обозначениях модель примет следующий вид:
в противном случае. При этих обозначениях модель примет следующий вид:
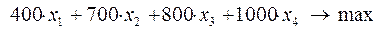
при ограничениях
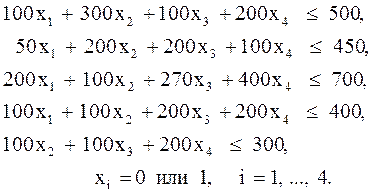
Здесь целевой функцией является суммарная чистая прибыль, а неравенства ограничивают ежегодно используемые средства. Решение дает
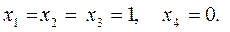
(следует принять первые три проекта). Отметим, что метод округления дает при этом неправильный результат – он рекомендует отвергнуть третий проект.
С помощью двоичных переменных легко формировать ограничения на базе логических условий, принимающих значения “истинно” или “ложно”.
Например, ограничение
 ,
,
где 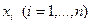 - двоичные переменные, а k – целое число, означает, что можно выбрать не более k из возможных n вариантов. Если в нашем примере руководство компании считает целесообразным принять не более одного зарубежного проекта и исключить варианты, включающие одновременно расширение завода в стране А и строительство нового завода в стране Б, то нужно добавить ограничение
- двоичные переменные, а k – целое число, означает, что можно выбрать не более k из возможных n вариантов. Если в нашем примере руководство компании считает целесообразным принять не более одного зарубежного проекта и исключить варианты, включающие одновременно расширение завода в стране А и строительство нового завода в стране Б, то нужно добавить ограничение
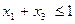 .
.
 2014-02-02
2014-02-02 954
954








