Движение газов при горении

Расширение газов в пламени (по закону Гей-Люссака) приводит к тому, что горение всегда сопровождается движением газов. Обозначим через ρ_г – плотность исходной среды, ρ_пр – плотность продуктов горения, их скорость по отношению к неподвижному фронту пламени равна u_пр. На каждый квад-ратный сантиметр поверхности фронта поток приносит ежесекундно u_н см³ горючей смеси, её масса равна u_н*ρ_г соответственно от этого участка пламени отводится в 1 сек u_пр см³ продуктов реакции с массой u_пр*ρ_пр. Поскольку мас-сы сгорающей смеси и продуктов реакции равны, то

u_н*ρ_г = u_пр*ρ_пр (7.10)

Уравнение (7.10) выражает закон сохранения массы при горении.

Величина u_пр превосходит нормальную скорость пламени во столько раз, во сколько плотность исходной среды больше плотности продуктов сгорания. Увеличение скорости газового потока при сгорании является след-ствием расширения газов.

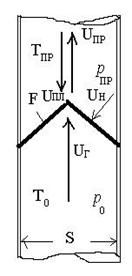
Абсолютная температура при сгорании повышается в 5–10 раз. Если горение происходит при постоянном давлении, газ расширяется в r_о/р_прраз. Рассмотрим горение стационарного фронта пламени в открытой трубе, изоб-раженной на рисунке 28.

	ρПР

ω

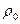Рис. 28. Схема пояснения закона площадей: S – сечение трубы, F – поверхность фронта пламени, ω - скорость исходной горючей смеси, Т₀,- тем­пература и плотность исходной смеси, U_H – нормальная скорость горения, U_ПЛ – скорость рас­-пространения пламени, U_ПР – скорость продуктов горения, Т_ПР, 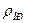- температура и плотность про-дук­тов горения.

Так как пламя располагается неподвижно, ω = U_ПР. Тогда, например, на 1 см² поверхности фронта пламени F поток приносит ω см³/с горючей смеси. Её масса равна ω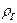. Соответственно от этого участка отводится U_ПР см³/с про­дуктов сгорания с массою U_ПР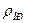. Тогда по закону сохранения масс (уравне­ние 7.10) при ω = U_ПЛ:

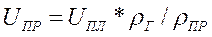(7.11)

Таким образом, объемная скорость продуктов сгорания превышает ско­-рость горения во столько раз, во сколько плотность исходной среды больше плотности продуктов горения.

С другой стороны, если на 1 см² поверхности фронта пламени сгорает U_Н см³/с смеси, то на всей площади F сгорает U_Н*F см³/с. В то же время объ-ем сгорающего газа равен объемной скорости газового потока ω*S см³/с. То-гда U_H*F = ω*S, или ω = U_H*F / S.

При равенстве ω =U_ПЛ:

U_ПЛ = U_H*F / S. (7.12)

Получаем закон площадей: скорость распространения пламени в трубе будет во столько раз больше нормальной, во сколько поверхность пламени превосходит поперечное сечение трубы.

Если рассматривать неподвижную горючую смесь, то при распростра­-нении фронта пламени резко нагретые газы не успевают расширяться, и в зо-не горения резко повышается давление, которое «распирает» и выталки­вает газы в обе стороны от пламени, причем выталкиваются не только про­дукты горения, но и возникает движение исходной смеси впереди фронта пламени, как на рисунке 29:

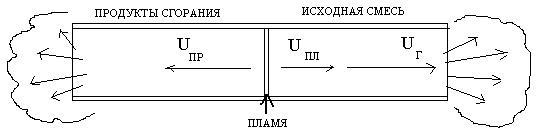
Рис. 29.

Скорость газов возрастает по мере сгорания исходной смеси и соответ­-ственно, давления газов. При этом с одного конца трубы выбрасываются сжа-тые раскаленные сгоревшие газы, а с другого выталкивается сжатая исходная смесь, которая взрывообразно воспламеняется от выброшенного пламени в атмосфере помещения с последующей ударной волной, пожаром и разруше­-нием.