Абсолютная температура, её определение и связь температурных шкал. Свойства абсолютной температуры

 

Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К). Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию. Абсолютный ноль определён как 0 K, что равно −273.15 °C.

2.Шкала Цельсия

В технике, медицине, метеорологии и в быту в качестве единицы измерения температуры используется шкала Цельсия. В настоящее время в системе СИ термодинамическую шкалу Цельсия определяют через шкалу Кельвина: t(°С) = Т(К) — 273,15 (точно), т. е. цена одного деления в шкале Цельсия равна цене деления шкалы Кельвина.

3.Шкала Фаренгейта

В Англии и, в особенности, в США используется шкала Фаренгейта. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а 100 градусов Цельсия — 212 градуса Фаренгейта.

В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 °F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 °F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением t °С = 5/9 (t °F — 32), t °F = 9/5 t °С + 32. Предложена Г. Фаренгейтом в 1724 году.

4.Шкала Реомюра

Предложена в 1730 году Р. А. Реомюром, который описал изобретённый им спиртовой термометр.

Единица — градус Реомюра (°Ré), 1 °Ré равен 1/80 части температурного интервала между опорными точками — температурой таяния льда (0 °Ré) и кипения воды (80 °Ré)

1 °Ré = 1,25 °C.

 

Связь температуры с кинетической энергией и скоростью движения молекул.

33.Уравнение Клапейрона-Менделеева. Постоянная Больцмана. Число Лошмидта.

 

Уравнение Клапейрона — Менделеева

Как уже указывалось, состояние некоторой массы газа определяется тремя термодина­мическими параметрами: давлением р,объемомVи температуройТ.Между этими параметрами существует определенная связь, называемаяуравнением состояния,кото­рое в общем виде дается выражением

где каждая из переменных является функцией двух других.

Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состоя­ния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V1,имеет давлениер1и находится при тем­пературеT1.Эта же масса газа в другом произвольном состоянии характеризуется параметрамир2, V2,T2(рис. 63). Переход из состояния1в состояние2осуществляется в виде двух процессов: 1) изотермического (изотерма1–1'),2) изохорного (изохора1'–2).

В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) за­пишем:

(42.1)

(42.2)

Исключив из уравнений (42.1) и (42.2) получим

Так как состояния 1и2были выбраны произвольно, то для данной массы газа величинаpV/Tостается постоянной, т. е.

(42.3)

Выражение (42.3) является уравнением Клапейрона,в которомВ —газовая постоянная,различная для разных газов.

Русский ученый Д. И. Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем Vm.Согласно закону Авогадро, при одинаковыхриТмоли всех газов занимают одинаковый молярный объемVm,поэтому постояннаяВбудетодинаковой для всех газов.Эта общая для всех газов постоянная обозначаетсяRи называется молярном газовой постоянной.Уравнению

(42.4)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа,называемым такжеуравнением Клапейрона — Менделеева.

Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях (р0=10×1,0135Па,T0=273,15 К,Vm10×=22,41–3м3/моль):RК).×=8,31 Дж/(моль

От уравнения (42.4) для моля газа можно перейти к уравнению Клапейро­на — Менделеева для произвольной массы газа. Если при некоторых заданных давле­нии и температуре один моль газа занимает молярный объем Vm,то при тех же условиях массатгаза займет объемV= (т/М)Vm, гдеМ — молярная масса(масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массытгаза

(42.5)

где n =m/M — количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:

Исходя из этого уравнение состояния (42.4) запишем в виде

где NA/Vm = n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

(42.6)

следует, что давление идеального газа при данной температуре прямо пропорциональ­но концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3газа принормальных условиях,называетсячислом Лошмидта*

 

34.Основные положения молекулярно-кинетической теории идеального газа и её основное уравнение.

 

Основное уравнение молекулярно-кинетической теории (МКТ) с выводом

В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.

Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ - разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:

молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости

при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания

Основное уравнение молекулярно-кинетической теории

Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа - это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:

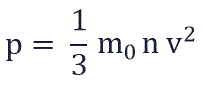
p – давление молекул газа на границы емкости,

m0 – масса одной молекулы,

n - концентрация молекул, число частиц N в единице объема V;

v2 - средне квадратичная скорость молекул.

Вывод основного уравнения МКТ

Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция vx скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:

Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv1x = –mvxна mv2x = mvx.

Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:

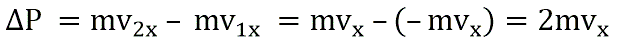
Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:

S – площадь этой стенки

n - концентрация частиц

 

Давление p равно отношению силы F к площади S, на которую действует эта сила:

Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:

Исходя из вышенаписанного получаем:

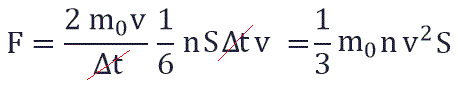
Тогда

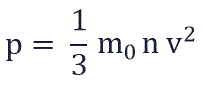
Если заменить среднее значение кинетической энергии поступательного движения молекул - E:

и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:

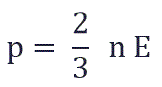
Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.