Ударные волны в инертном газе

Ударное сжатие. При любом резком повышении давления в газе или жидкости возникает волна сжатия – ударная волна. Она распространяется по сжимаемой среде, переводя ее в более плотное состояние. Ударная волна представляет собой границу скачкообразного перехода от состояния исходно-го вещества к состоянию сжатого. В сильных ударных волнах это изменение происходит на расстоянии порядка длины свободного пробега молекул. Воз-никновение волны сжатия обусловлено тем, что изменившееся в какой-либо точке пространства давление выравнивается не мгновенно, а с конечной, хотя и достаточно большой скоростью, порядка скорости звука в данной среде.

Для определения закономерностей ударного сжатия рассмотрим пове-дение однородного газа, находящегося в длинной трубе, при быстром вдви-жении в трубу поршня. Труба достаточно широка и сжатие достаточно быст-ро для того, чтобы теплоотдачей от сжатого газа к стенкам трубы и к несжа-тому газу можно было пренебречь и не учитывать торможение газового пото-ка трением у стенок.

Принимаем, что поршень движется с постоянной скоростью w:очевид-но, что это – скорость движения сжимаемого газа. Граница между сжатым и несжатым газом, т. е. волна сжатия, движется по отношению к исходному, не-сжатому газу впереди поршня со скоростью D. Скорость распространения волны сжатия определяется условием сохранения при прохождении волны трех характеристик: массы, количества движения и энергии.

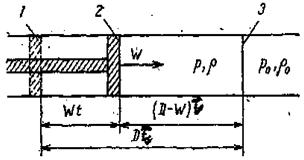
Рис. 31. Схема движения волны сжа-тия: 1 – исходное положение поршня; 2–положение поршня в момент времени τ; 3– положение фронта ударной волны в момент времени τ.

Схема движения волны сжатия и газа показана на рис. 31. Обозначим через v = 1/ρ удельный объем, ρ – плотность газа.За время τ поршень, а с ним и газ переместится на расстояние wτ, волна сжатия – на расстояние Dτ по отношению к исходному положению поршня и на расстояние (D- w)τ – к ко-нечному; (D - w)τ – высота столба сжатого газа. Расстояние, пройденное вол-ной, определяет объем сжатого вещества в его исходном состоянии; здесь и в дальнейшем расчет ведется на единицу поверхности поршня. После сжатия объем этого количества вещества сокращается до границ между фронтом волны и поршнем (D- w) τ, в силу закона сохранения массы

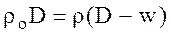(8.1)

При переходе в сжатое состояние масса вещества, равная r_оD τ,приобрела скорость w. Произведение этих величин представляет собой изменение количества движения, которое, согласно второму закону Ньютона, равно им-пульсу действующей силы, определяемой изменением давления при сжатии; импульс силы равен (P– P_о) τ,т. е.

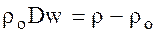(8.2)

По условию сжатие не сопровождается теплообменом, и в силу закона сохранения энергии величина изменения полной энергии единицы массы газа равна затраченной при этом процессе работе. На пути wτ поршень действовал на газ с силой P. При этом был сжат столб газа с массой r_оD τ, изменение внутренней энергии единицы его массы равно Е – Е_о, а кинетической энергии w²/2. Отсюда следует, что

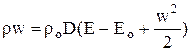(8.3)

Уравнение (8.1) дает соотношение скоростей D и w:

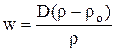(8.1а)

Из уравнения (8.1а) очевидно, что при ударном сжатии к заметному из-менению плотности приводит только такое движение газа, скорость которого соизмерима со скоростью ударной волны.

Уравнения (8.1) и (8.2) без использования уравнения сохранения энер-гии связывают скорость волны, возникающей при ударном сжатии, либо не-обходимую для этого скорость движения газа с параметрами состояния сжа-того вещества P, v:

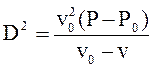(8.4)

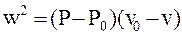(8.5)

Из уравнений (8.3), (8.1а) и (8.5) следует:

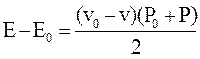(8.6)

Адиабата Гюгонио. Полученные выражения и уравнение термодинамического состояния газа, связывающее между собой значения T, Pи v, позволяют описать ударное сжатие от P_o, v_oдо P,vкривой в координатах P – v,которая называется адиабатой (сжатие происходит без теплообмена) Гюгонио. Величины исходных давления и удельного объема, имеющие особое значение, содержатся в уравнении адиабаты Гюгонио в качестве параметров.

Закономерности сжатия в ударной волне принципиально отличаются от закономерностей изоэнтропического сжатия, описываемого адиабатой Пуас-сона:

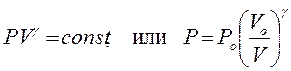. (8.7)

Изоэнтропическое сжатие обратимо, его можно выполнять ступенчато, после-довательно сжимая газ от Р_одо Р₁> Р_о, затем до Р₂ > Р₁ и т. д., а также чередуя сжатие и разрежение; при этом достигается то же конечное состояние. Как при всяком обратимом процессе, результат сжатия по адиабате Пуассона не зависит от порядка ведения процесса, а лишь от начального и конечного дав-лений.

Ударное сжатие необратимо и потому неизоэнтропично, часть энергии сжатия расходуется на необратимое нагревание газа. Разделим ударное сжа-тие от Р_о до Р₂ на два этапа: первая ударная волна сжимает газ от Р_о до Р₁ < Р₂, вторая – от Р₁ до Р₂ (рис. 32). Состояние Р₁, v будет играть роль исходного для второй ударной волны. При этом конечный объем v₂, меньше соответствую-щей величины v₂, характеризующей состояние вещества при одностадийном сжатии до Р₂. Поэтому при сжатии по адиабате Гюгонио вещество не прохо-дит через состояния, соответствующие последовательному перемещению вдоль кривой Р(v), как это происходит при изоэнтропическом сжатии. Эта кривая лишь определяет конечное значение удельного объема при ударном сжатии газа с параметрами Р_о, v_о до давления Р.

Давление газа в ударной волне отличается от давления в неподвижном газе. Давление на стенку зависит также от ее ориентации по отношению к на-правлению движения ударной волны. Поэтому закон Паскаля здесь не вы-полняется.

При стационарном распространении ударной волны, т. е. при D = const, в зоне изменения плотности существует линейная зависимость между вели-чинами давления и удельного объема, как это следует из уравнения (8.4).

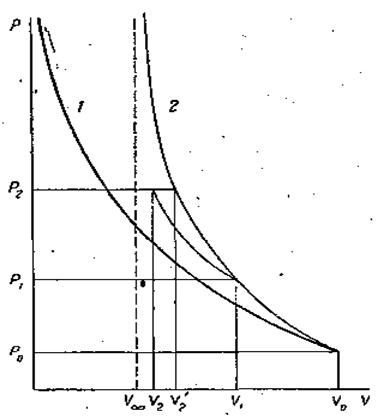
Рис. 32. Адиабаты Гюгонио и Пуассона: 1 -адиабата Пу-ассона; 2 – адиабата Гюго-нио.

Из уравнения (8.4) следует также, что скорость ударной волны возрас-тает с увеличением степени сжатия. Очевидно, что скорость ударной волны определяется наклоном прямой, связывающей точки Р, v и Р_о, v_о. Если сред-нее в диапазоне v_о–v значение углового коэффициента (для прямой Р – v) рав-но ΔР/Δv, то

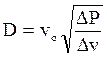(8.8)

В предположении Е = c_vT, и учитывая, что c_p/c_v = g, с_р – c_v = R/M (M – молекулярная масса), а RT = РvM, найдем

(8.9)

Выражая аналогично величину Е_ои используя уравнения (8.6), запишем уравнение адиабаты Гюгонио в наиболее удобной форме:

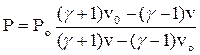(8.10)

В координатах Р – vадиабата Гюгонио изображается более крутой кри-вой, чем адиабата Пуассона (см. рис. 33). Умножая обе части уравнения (8.10) на отношение v/v_о,можно вычислить степень нагревания в ударной волне, учитывая, что Т/Т_о = Рv/Р_ov_o:

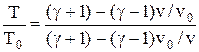(8.11)

Сильные и слабые ударные волны. Существенная особенность удар-ного сжатия заключается в том, что, как бы ни было высоко давление в удар-ной волне, степень сжатия 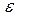= v_o/vне может превысить некоторого конеч-ного значения. При Р>>Р_о, v → v_∞

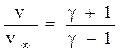(8.12)

При изоэнтропическом сжатии объем неограниченно уменьшается с ростом конечного давления (см. рис. 32). Если в каждой из п последователь-ных ударных волн Р >> Р_о,то

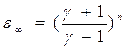(8.13)

Из уравнений (8.4) и (8.5) вытекают и другие особенности сжатия в сильной ударной волне. Полагая Р >> Р_ои подставляя в эти уравнения значе-ние ε_∞, находим

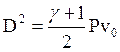(8.14)

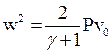(8.15)

Таким образом, при сильном сжатии рост давления в ударной волне пропорционален квадрату скорости сжимающего тела (поршня).

Не только очень сильные, но и очень слабые ударные волны отличаются рядом особенностей. Ударное сжатие очень малой амплитуды эквивалентно сжатию в звуковой волне. В этом случае D = с_о, где с_о – скорость звука в ве-ществе, находящемся в исходном состоянии. В этом случае разности Р–Р_о=ΔР и v_о–v=Δv можно заменить дифференциалами, аналогичные суммы – величи-нами 2Р и 2v либо 2Р_о и 2v₀ соответственно. Уравнение (8.4) принимает вид:

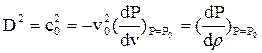(8.16)

Скорость движения газа в слабой ударной волне, как это следует из уравнений (8.4) и (8.5), мала по сравнению со скоростью волны. Для слабого сжатия адиабаты Гюгонио и Пуассона совпадают.

Для звуковой волны, как следует из уравнения (8.6),

dE = - Рdv (8.17)

В предельном случае сильного сжатия по уравнению (8.12) рост темпе-ратуры, как это следует из уравнения (8.11), равен

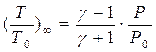(8.18)

т.е. Т ~ Р,тогда как при изотермическом сжатии (уравнение 7.9) показатель степени при Р,равный (g — 1)/g, не превосходит 0,4. Так, при Р/Р_о = 100 для двухатомного газа (Т/Т₀)_∞ = 16,6, аналогичная величина для изоэнтропическо-го сжатия имеет значение (T/T₀)i = 3,72.

Поскольку сжатие в звуковой волне изоэнтропично, очевидно, что для идеального газа (т.е. для условия Р=const Р^g)

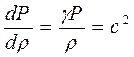(8.19)

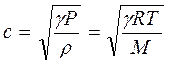(8.20)

Скорость звука возрастает с повышением температуры газа ~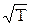, поэтому для газа, сжатого ударной волной, с > с₀. Подставляя в уравнение (8.19) зна-чение плотности при сильном сжатии, найдем скорость звука для этого ре-жима:

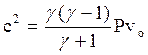(8.21)

Сопоставление уравнений (8.14), (8.15) и (8.22) показывает, что при сжатии в сильной волне текущее значение скорости звука составляет 41-56% скорости ударной волны, а скорость газа, стремящаяся к нулю для слабых волн, достигает 75-86% скорости ударной волны. Скорость сильной ударной волны значительно больше скорости звука в несжатом газе:

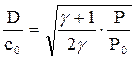(8.22)

Так, при Р/Р_о= 100 для одноатомного газа D = 8с_о.

Структура ударной волны. Установленные закономерности позволяют объяснить важную особенность сжатия в ударной волне – резкое изменение свойств сжимаемого вещества. Рассмотрим сжатие газа в описанном в начале главы опыте с вдвижением поршня в трубу при условии его ускорения, при-чем скорость поршня возрастает последовательными небольшими скачками.

После первого увеличения скорости поршня от нуля до определенного малого значения w₁ возникает слабая ударная волна, движущаяся по сжимае-мому газу со скоростью D₁. При увеличении скорости поршня до w₂>w₁ воз-никает новая ударная волна, распространяющаяся по уже сжатому газу со скоростью D₂. Легко показать что D₂>D₁. С одной стороны, скорость слабой ударной волны, близкая к скорости звука, возрастает с повышением темпера-туры и потому будет больше в газе, уже нагретом первой волной. С другой стороны, сам сжатый газ движется в направлении распространения волны сжатия.

Поскольку скорость второй ударной волны больше первой, через опре-деленное время вторая волна догонит первую. Обе волны сольются, их ам-плитуды сложатся, две волны заменятся одной новой, более мощной. Анало-гичным образом происходит наложение всех последующих волн, а также бес-конечно малых волн, возникающих при плавном ускорении поршня, с обра-зованием все более сильной волны. Наложение последовательно распростра-няющихся ударных волн является причиной резкого изменения свойств сжи-маемого ими газа, ударная волна имеет характер разрыва, скачка.

Ширина фронта очень слабых волн может быть довольно значительна. Для сильной ударной волны, т.е. при Р >> Р_о,фронт волны имеет ширину по-рядка длины свободного пробега.

Поведение ударной волны у преграды. Для техники безопасности имеют большое значение закономерности отражения ударной волны от не-подвижной преграды. В силу относительности движения торможение газа, сжатого ударной волной, у препятствия, нормального направлению распро-странения волны, эквивалентно движению этой стенки в обратном направле-нии по неподвижному газу. При этом она как поршень повторно сжимает газ, уже сжатый исходной, падающей волной. Встреча ударной волны с непод-вижной стенкой приводит к образованию отраженной ударной волны и еще более сильному сжатию газа.

Для слабых волн давление в отраженной волне вдвое больше, чем в па-дающей волне. При большем сжатии это различие возрастает.

Если Р₊ >> Р_о, то

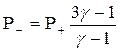, (8.23)

где: Р_- и Р₊ - давления газа соответственно в отраженной и прямой волне, так для двухатомного газа, т.е. для g = 7/5, давление в сильной отраженной волне в 8 раз превосходит давление в падающей волне.

Таким образом, отражение ударной волны от преграды может приво-дить к чрезвычайно высокому, хотя и кратковременному росту давления, ко-торый способен вызвать большие разрушения. Следует иметь в виду, что роль преграды, отражающей ударную волну, могут играть не только стенки сосуда или стены закрытого помещения, но и любое твердое тело, оказывающееся на пути распространения ударной волны.

Необходимо отметить, что к разрушениям промышленных и жилых зданий и сооружений может приводить уже сравнительно небольшой рост давления в ударной волне, если только волна отличается большими геометри-ческими размерами, т. е. действует на большие площади. Волна с амплитудой 0,35 am разрушает здания, а при нескольких сотых am выбивает окна. Чело-век может перенести действие ударной волны около 0,5 am, если не будет брошен ею на землю. Ускорение, полученное человеком под действием удар-ной волны, может быть настолько велико, что удар о землю оказывается смертельным.