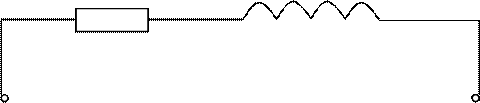
Пусть в электрической цепи с резистивным (активным) R и индуктивным L элементами (рис. 5.10) ток изменяется по синусоидальному закону:
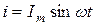 . (5.14)
. (5.14)
Для упрощения начальная фаза тока принята равной нулю (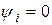 ).
).
UR UL

 L i
L i
U

Рис.5.10
Согласно (5.6) напряжение на резистивном элементе 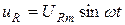 и совпадает по фазе с током
и совпадает по фазе с током  . Согласно (5.8) напряжение на индуктивном элементе
. Согласно (5.8) напряжение на индуктивном элементе 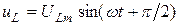 и по фазе опережает током
и по фазе опережает током  на угол
на угол 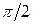 . С учетом вышеизложенного построим векторную диаграмму (рис.5.11,а) для рассматриваемой цепи.
. С учетом вышеизложенного построим векторную диаграмму (рис.5.11,а) для рассматриваемой цепи.
 | |||
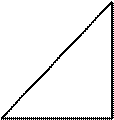 | |||
Um ULm Z XL
 φ URm φ R
φ URm φ R


Рис.5.11,а Рис.5.11,б
На векторной диаграмме суммарное напряжение 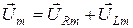 на активном R и индуктивном L элементах
на активном R и индуктивном L элементах 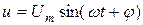 изображается вектором
изображается вектором 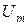 , сдвинутым по фазе относительно вектора тока на угол
, сдвинутым по фазе относительно вектора тока на угол 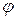 . Векторы
. Векторы  и
и 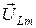 образуют треугольник напряжений. Для него на основании теоремы Пифагора имеем:
образуют треугольник напряжений. Для него на основании теоремы Пифагора имеем:
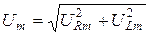 . (5.15)
. (5.15)
Но поскольку 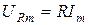 , а
, а 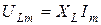 , то (4.15) может быть преобразовано:
, то (4.15) может быть преобразовано:
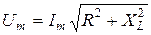 , или
, или 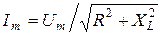 , (5.16)
, (5.16)
где 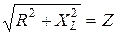 – полное сопротивление цепи. Тогда закон Ома для рассматриваемой цепи и амплитудных значений тока и напряжения:
– полное сопротивление цепи. Тогда закон Ома для рассматриваемой цепи и амплитудных значений тока и напряжения: 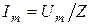 или для действующих значений:
или для действующих значений:
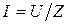 . (5.17)
. (5.17)
Поскольку полное сопротивление определяется по теореме Пифагора, то ему соответствует треугольник сопротивлений, приведенный на рис. 5.11,б. Сдвиг фаз между током и напряжением 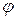 определяется из треугольника сопротивлений:
определяется из треугольника сопротивлений:
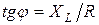 или
или 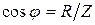 .
.
 2014-02-02
2014-02-02 571
571








