2014-02-02
1873
Пусть в электрической цепи с индуктивным элементом L (рис. 5.7) ток изменяется по синусоидальному закону:
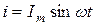. (5.7)
Для упрощения начальная фаза тока принята равной нулю (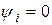
). Из-за переменного характера тока происходит изменение потока Ф, пронизывающего катушку индуктивности. В результате чего в ней наводится ЭДС самоиндукции 
.
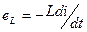i L
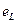
UL
Рис.5.7
Поскольку цепь содержит только индуктивный элемент и активное сопротивление цепи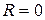 
, то напряжение 
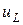, на полюсах индуктивного элемента L, целиком идет на уравновешивание ЭДС самоиндукции, т.е. 
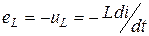. Откуда 
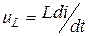. Переписав последнее выражение с учетом синусоидального характера изменения тока, получим:
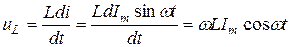, или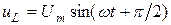 
, (5.8)
где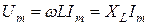 
, 
– индуктивное сопротивление индуктивного элемента L. Размерность индуктивного сопротивления – (Ом).
Из анализа выражений (5.7) и (5.8) следует, что напряжение 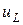опережает ток 
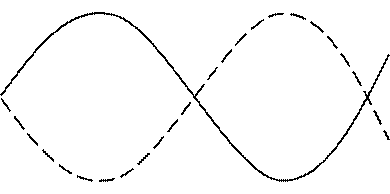
на угол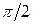 
. Векторная и угловая диаграммы тока, напряжения и ЭДС на индуктивном элементе приведены на рис. 5.8.
|
 |
|
Im 
Um Um
 |
π/2 Im π 2π
-π/2 0 π/2 ωt
|
|
|
3π/2 
Рис.5.8
Преобразовав (4.8) получим закон Ома для рассматриваемой цепи:
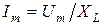, (5.9)
или поделив амплитудные значения тока и напряжения на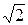 
получим закон Ома для действующих значений:
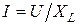. (5.10)
