Методы первого порядка

Методы первого порядка используют, если возможно найти первую про­изводную исследуемой функции. К данному классу относятся градиентные методы. Их суть заключается в определении лучшего направление и шага поиска минимума функции по значениям первых производных в некото­рой точке 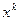. Наибольшее значение производной показывает направление наискорейшего уменьшения функции, и в этом направлении рассчитыва­ется следующее приближение функции 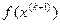, параметры которой отличаются на величину некоторого шага 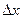. В зависимости от способа задания этого шага и производится классификация градиентных методов: гра­диентный спуск; наискорейший спуск; градиентный спуск постоянным шагом; градиентный спуск с переменным шагом. Методы эффективны для функций со слабовыраженной нелинейностью.