Обучение доказательству

Доказательство противоречием. Обращение по разделению.

Нисходящий анализ.

Восходящий анализ.

Синтетический метод доказательства.

Математическая индукция.

Дедуктивный метод доказательства. Силлогизмы.

Доказательство. Виды доказательств.

МЕТОДЫ ДОКАЗАТЕЛЬСТВА ТЕОРЕМ. МЕТОДИКА ОБУЧЕНИЯ ШКОЛЬНИКОВ ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ

ЛЕКЦИЯ №6

Вопросы:

ОПРЕДЕЛЕНИЕ. Под доказательством мы будем понимать логическое действие, в процессе которого истинность суждения обосновывается с помощью других суждений, которые считаются истинными.

Многовековой опыт убедил людей в том, что доказательство является одним из важнейших свойств правильного мышления, которое приводит к истинному знанию. Доказывать приходится не только в математике. Поэтому возникла целая наука, которая занимается доказательством. Эта наука - логика. В ней доказательство рассматривается отвлеченно, абстрагируясь от конкретного содержания той или иной теоремы, и дает некоторые общие рекомендации, которые используются при любом доказательстве. Однако нет универсального метода доказательства, которое бы годилось во всех случаях.

Во всяком доказательстве логика выделяет три составляющие:

1) тезис - суждение, истинность которого требуется установить;

2) довод - суждение, истинность которого известна и которое может быть приведено в качестве обоснования истинности или ложности тезиса;

3) демонстрация - логическое рассуждение, в процессе которого из доводов выводится истинность или ложность тезиса, а также совокупность логических правил, используемых в доказательстве.

По способу ведения доказательства подразделяются на прямые и косвенные.

Доказательство называется прямым, если истинность тезиса выводится непосредственно из истинного довода.

Доказательство называется косвенным (непрямым), если истинность тезиса обосновывается путем опровержения истинности противоречащего тезису суждения. К косвенным доказательствам относятся:

1) доказательства методом «от противного»;

2) разделительные доказательства.

Доказательство называется разделительным, если тезис этого доказательства является разделительным суждением вида «Т есть или Р₁, или Р₂, …, или Р_n», где число различных случаев n конечно и не менее двух. Последовательно исключая все суждения Р_i, кроме одного, который нужно доказать, получаем доказательство теоремы. Приведем пример теоремы школьного курса математики, где используется как прямое, так и разделительное доказательства.

ТЕОРЕМА. Выпуклый четырехугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов этого четырехугольника равна 180^о.

Доказательство. Пусть четырехугольник вписан в окружность. Тогда сумма противоположных углов этого четырехугольника равна 180^о.

Обратно, пусть сумма противоположных углов четырехугольника АВСД, например, ÐА + ÐС = 180^о. Опишем около треугольника АВД окружность. Тогда для точки С возможны три случая:

а) точка С - внутри круга;

б) точка С - на окружности;

с) точка С - вне круга.

Покажем, что случаи а) и с) невозможны.

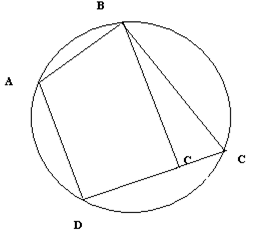Пусть выполняется случай а). Пусть С₁ - точка пересечения стороны ДС с описанной окружностью. Тогда четырехугольник АВС₁Д является вписанным, а, значит ÐА + ÐС₁ = 180^о. Отсюда ÐВСД = ÐВС₁Д. Получаем противоречие, ибо ÐВСД является внутренним для треугольника ВС₁С, а ÐВС₁Д -внешним.

Пусть выполняется случай с). Пусть С₁ - точка пересечения продолжения стороны ДС с описанной окружностью. Тогда четырехугольник АВС₁Д является вписанным, а, значит ÐА + ÐС₁ = 180^о. Отсюда ÐВСД = ÐВС₁Д. Получаем противоречие, ибо ÐВС₁Д является внутренним для треугольника ВС₁С, а ÐВСД -внешним. Теорема доказана.

По форме умозаключения, в которой совершаются доказательства, различают индуктивные и дедуктивные доказательства. Индуктивные доказательства получаются в результате применения полной индукции или математической индукции. Математическая индукция будет рассмотрена в дальнейшем, а сейчас остановимся подробнее на полной индукции.

Умозаключением называют мыслительную операцию, в результате которой из одного или нескольких известных нам суждений, находящихся в определенной смысловой зависимости, получают новое суждение, содержащее новое по отношению к исходным суждениям знание.

Умозаключение, в результате которого получается общий вывод обо всех элементах множества на основании знания обо всех без исключения элементах данного множества, называется полной индукцией.

Общую схему полной индукции во множестве М можно записать так:

К₁ есть Р

К₂ есть Р

….

К_n есть Р

{К₁, К₂, …, К_n} = М

Все К есть Р.

Приведем пример.

ТЕОРЕМА. Величина вписанного угла равна половине дуги, на которую она опирается.

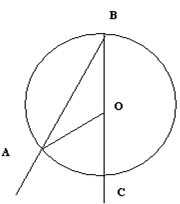Доказательство. Пусть угол ÐАВС вписан в окружность. Рассмотрим три возможных случая:

1) центр окружности - точка О - на стороне ВС;

2) О внутри угла АВС;

3) О вне угла АВС.

В первом случае проведем АО. Тогда ÐАОС - внешний для треугольника АВО. Кроме того, DАВО является равнобедренным. Отсюда ÐАВС = 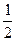ÐАО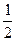С = АС.

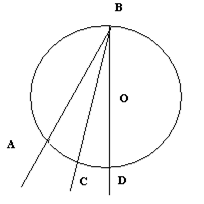
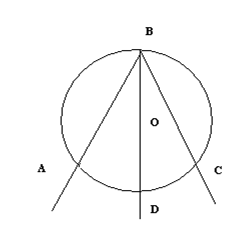Во втором случае проведем луч ВО, который пересечет окружность в точке Д. Тогда ÐАВС = ÐАВД + ÐДВС = 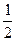(АД + Д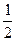С) = АС.

В третьем случае аналогично проведем луч ВД. Тогда ÐАВС = ÐАВД - ÐСВД = 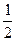(АД - Д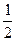С) = АС.

Видно, что при доказательстве этой теоремы рассматриваются все три возможных случая расположения центра окружности относительно данного вписанного угла, и каждый случай строго обосновывается.

Доказательство называется дедуктивным, если оно представляет собой цепочки дедуктивных силлогизмов, каждый из которых представляет собой вывод частного из общего, т.е. проводится по схеме