Достоверность, сходимость и воспроизводимость измерений

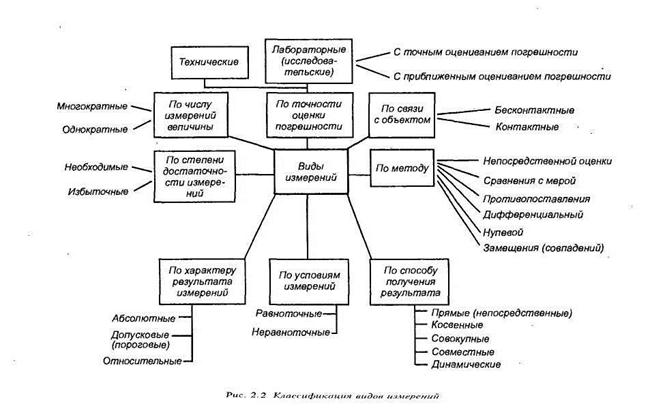
Классификация измерений.

Цель измерения — получение значения величины в форме, наиболее удобной для пользования. С помощью измерительного прибора сравнивают размер величины, информация о котором преобразуется в перемещение указателя, с единицей, хранимой шкалой этого прибора.

Измерения весьма разнообразны и классифицировать их можно по различным признакам.

В настоящее время принята следующая классификация:

- по характеристике точности — равноточные, неравноточные;

- по числу измерений в серии — однократные и многократные;

- по отношению к изменению измеряемой величины — статические и динамические;

- по метрологическому назначению — технические и метрологические;

- по выражению результата измерений — абсолютные и относительные;

- по общим приемам получения результатов измерений — прямые, косвенные, совместные, совокупные.

Равноточные измерения — ряд измерений какой-либо величины, выполняемых одинаковыми по точности средствами измерений в одних и тех же условиях. Если одно из этих условий не выполняется, то измерения называют неравноточными.

Однократное измерение — измерение, выполняемое один раз. Например, определение времени по часам. Если необходима большая уверенность в получаемом результате, то проводятся многократные измерения, результат которых получают из нескольких следующих друг за другом измерений. За результат многократного измерения обычно принимают среднее арифметическое значение из результатов однократных измерений, входящих в ряд.

Статическое измерение — измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Например, измерение длины детали при нормальной температуре. Если размер физической величины изменяется с течением времени, то такие измерения называют динамическими. Примером таких измерений может быть определение расстояния до поверхности земли со снижающегося самолета.

Технические измерения обычно используются в ходе контроля при изготовлении изделий, технологических процессов. Например, измерение давления пара в котле при помощи манометра. Обычно они выполняются с помощью рабочих средств измерений.

Метрологические измерения предназначаются для воспроизведения единиц физических величин или для передачи их размера рабочим средствам измерений. В ходе их выполнения используются эталоны или образцовые средства измерений.

Абсолютное измерение — измерение, приводящее к значению измеряемой величины, выраженному в ее единицах. При измерении длины детали штангенциркулем результат выражается в единицах измеряемых величин (в миллиметрах).

В относительных измерениях измеряется отношение величины к одноименной величине, играющей роль единицы или измерения величины по отношению к одноименной величине, принимаемой за исходную. Примером может служить измеритель скорости у сверхзвуковых самолетов, показывающий отношение скорости самолета к скорости звука или указатели расхода бензина в автомобилях.

Подробнее рассмотрим прямые, косвенные, совместные и совокупные измерения.

К прямым относятся измерения, результаты которых получают с помощью средств измерений, находящихся под воздействием данной измеряемой величины, проградуированной непосредственно в единицах этой величины. При проведении этих измерений, как правило, не требуется проведения каких-либо вычислений.

Математически прямое измерение может быть представлено в виде уже приводившейся формулы (1.1) Числовое значение X, характеризующее разряд величины Q выраженной в единицах [Q], определяется непосредственно по показаниям мер или измерительных приборов, предназначенных для измерений данной величины Q.

Примером прямых измерений могут быть измерения длины линейкой, времени при помощи часов, массы при помощи гирь на равноплечих весах, температуры — термометром, силы тока — амперметром и т. д.

Прямое измерение может также заключаться в однократном применении измерительного прибора с непосредственным отсчетом по нему результата, но может включать и несколько повторных наблюдений с вычислением результата как среднего из нескольких измерений. Для получения результата также может потребоваться умножение отсчета по шкале измерительного прибора на цену деления.

Косвенными называют измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, определяемыми прямыми измерениями. Результат находят из решения уравнения, выражающего эту зависимость. Косвенное измерение можно описать уравнением

Q = f (X, Y, Z, W)

где Q — измеряемая величина; X, Y, Z, W — величины, размер которых определяется из прямых измерений. В этом уравнении (X, У, Z) представляют конкретные реализации величин, связанных с некоторым определенным объектом. Рассмотрим пример. Требуется измерить удельное электрическое сопротивление некоторого материала. Но так как приборов для прямых измерений удельного сопротивления нет, его можно измерить только косвенным методом.

Совокупными измерениями называют одновременные измерения нескольких одноименных величин, при которых искомое значение находят решением системы уравнений, получаемых в результате прямых измерений различных сочетаний этих величин.

Совместными называют производимые одновременно (прямые и косвенные) измерения двух и более разноименных величин. Целью таких измерений является, фактически, определение функциональной связи между величинами.

В метрологии, использующей теорию вероятностей, основными величинами являются отдельные значения случайных величин, а производными — мера их рассеивания (дисперсия) и др.

Понятие о методах измерений.

Метод измерений — прием или совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений.

Методы измерений классифицируют по нескольким признакам. По общим приемам получения результатов измерений различают: 1) прямой метод измерений; 2) косвенный метод измерений. Первый реализуется при прямом измерении, второй — при косвенном измерении, которые описаны выше.

По условиям измерения различают контактный и бесконтактный методы измерений.

Контактный метод измерений основан на том, что чувствительный элемент прибора приводится в контакт с объектом измерения (измерение температуры тела термометром). Бесконтактный метод измерений основан на том, что чувствительный элемент прибора не приводится в контакт с объектом измерения (измерение расстояния до объекта радиолокатором, измерение температуры в доменной печи пирометром).

Исходя из способа сравнения измеряемой величины с ее единицей, различают методы непосредственной оценки и метод сравнения с мерой.

При методе непосредственной оценки определяют значение величины непосредственно по отсчетному устройству показывающего СИ (термометр, вольтметр и пр.). Мера, отражающая единицу измерения, в измерении не участвует. Ее роль играет в СИ шкала, проградуированная при его производстве с помощью достаточно точных СИ.

При методе сравнения с мерой измеряемую величину сравнивают с величиной, воспроизводимой мерой (измерение массы на рычажных весах с уравновешиванием гирями). Существует ряд разновидностей этого метода: нулевой метод, метод измерений с замещением, метод совпадений.

Вынесенные в заголовок учебного вопроса понятия призваны характеризовать качество измерений.

Под качеством измерений понимают совокупность свойств, обусловливающих получение результатов с требуемыми точностными характеристиками, в необходимом виде и в установленные сроки. Качество измерений характеризуется такими показателями, как точность, правильность и достоверность. Эти показатели должны определяться по оценкам, к которым предъявляются требования состоятельности, несмещенности и эффективности.

Истинное значение измеряемой величины отличается от среднего значения на величину систематической погрешности ,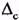

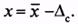
Если систематическая составляющая исключена, то 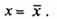Однако из-за ограниченного числа наблюдений х точно определить также невозможно. Можно лишь оценить это значение, указать границы интервала, в котором оно находится, с определенной вероятностью.

Оценку x числовой характеристики закона распределения х изображаемую точкой на числовой оси, называют точечной оценкой. В отличие от числовых характеристик оценки являются случайными величинами. Причем их значение зависит от числа наблюдений п.

Состоятельной называют оценку, которая сводится по вероятности к оцениваемой величине, т.е.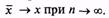

Несмещенной является оценка, математическое ожидание которой равно оцениваемой величине, т.е.

Эффективной называют такую оценку, которая имеет наименьшую дисперсию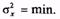

Перечисленным требованиям удовлетворяет среднее арифметическое х результатов п наблюдений.

Таким образом, результат отдельного измерения является случайной величиной. Тогда точность измерений — это близость результатов измерений к истинному значению измеряемой величины.

Если систематические составляющие погрешности исключены, то точность результата измерений Зσ характеризуется степенью рассеяния его значения, т. е. дисперсией. Как показано выше (см. формулу 2.4), дисперсия среднего арифметического а* в п раз меньше дисперсии отдельного результата наблюдения.

На рис. 2.9 заштрихованная площадь относится к плотности вероятности распределения среднего значения.

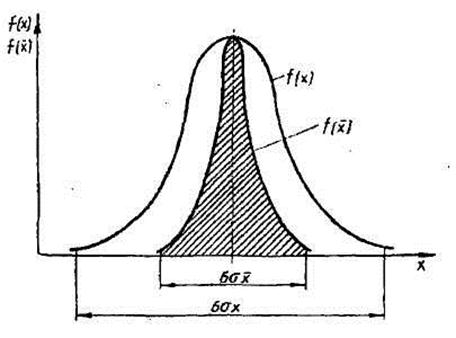
Рис. 2.9. Плотность распределения отдельного и суммарного результата измерения

Правильность измерений определяется близостью к нулю систематической погрешности.

Достоверность измерений зависит от степени доверия к результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в указанных окрестностях действительного.

Следует отметить, что результаты измерений, не обладающие достоверностью, т. е. степенью уверенности в их правильности не представляют ценности. Например, датчик измерительной схемы может иметь весьма высокие метрологические характеристики, но влияние погрешностей от его установки, внешних условий, методов регистрации и обработки сигналов приведет к большой конечной погрешности измерений.

Наряду с такими показателями, как точность, достоверность и правильность, качество измерительных операций характеризуется также сходимостью и воспроизводимостью результатов. Эти показатели наиболее распространены при оценке качества испытаний и характеризуют точность испытаний.

Очевидно, что два испытания одного и того же объекта одинаковым методом не дают идентичных результатов. Объективной мерой их могут служить статистически обоснованные оценки ожидаемой близости двух или более числа результатов, полученных при строгом соблюдении методики испытаний. В качестве таких статистических оценок согласованности результатов испытаний принимаются сходимость и воспроизводимость.

Сходимость (повторяемость) — это близость результатов двух испытаний, полученных одним методом, на идентичных установках, в одной лаборатории. Воспроизводимость отличается от сходимости тем, что оба результата должны быть получены в разных лабораториях. При доверительной вероятности Р= 0,95 сходимость определяется как r= 2,77σ_сх, а воспроизводимость — R = 2,77σ_в.

Здесь σ_сх и σ_в — стандартные отклонения результатов испытаний соответственно в условиях сходимости и воспроизводимости:

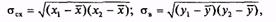
где х₁ и х₂ — результаты единичных испытаний в условиях сходимости; у₁ и у₂ — результаты единичных испытаний в условиях воспроизводимости; 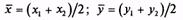— средние значения.

Отдельные стандарты задают значения r и R.

Прецизионность зависит только от случайных погрешностей и не имеет отношения к истинному или опорному значению измеряемой величины. Меру прецизионности обычно выражают в терминах неточности и вычисляют как стандартное отклонение результатов измерений. Меньшая прецизионность соответствует большему стандартному отклонению. Количественные значения мер прецизионности существенно зависят от регламентированных условий. Крайними случаями таких условий являются условия повторяемости и условия воспроизводимости.

Повторяемость — прецизионность в условиях повторяемости. В отечественных НД наряду с термином «повторяемость» используют термин «сходимость».

Условия повторяемости (сходимости) — условия, при которых независимые результаты измерений (или испытаний) получаются одним и тем же методом на идентичных объектах испытаний, в одной и той же лаборатории, одним и тем же оператором, с использованием одного и того же оборудования, в пределах короткого промежутка времени. В качестве мер повторяемости (а также воспроизводимости) в Стандарте 5725 используются стандартные отклонения.