Характеризация реберных графов

Граф G называется реберным графом, если он изоморфен реберному графу L(H) некоторого графа Н. Например, K4 - х есть реберный граф

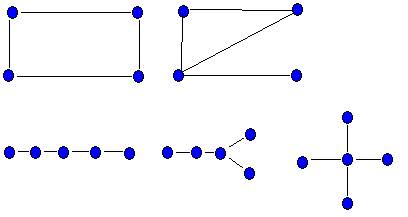
Покажем, что звезда К_1,3 не является реберным графом. Предположим, что K_1,3=L(H). Тогда граф H имеет 4 ребра, поскольку в K_1,3 четыре вершины, и, кроме того, граф H должен быть связным. Все связные графы с четырьмя ребрами приведены на рис. Так как L(С4)=С4 и L(K_1,3+x)=K₄ - х, то H может быть только одним из трех деревьев. Но реберными графами этих деревьев являются соответственно простая цепь Р4, граф К₃* К₂ и граф К₄. Таким образом К_1,3 не есть реберный граф. В дальнейшем мы увидим, что граф К_1,3 играет важную роль при установлении основных свойств реберных графов. Первый результат о реберных графах — утверждение (2) приведенной ниже теоремы -полученный Крауцем, довольно близок к самому определению реберного графа. Существенный сдвиг в изучении свойств реберных графов был сделан ван Роои и Вилфом, которым удалось получить (утверждение (3)) структурный критерий того, что данный граф является реберным. Наконец, Байнеке [4] и Робертсон (не опубликовано) нашли все подграфы, которые не могут встречаться в реберных графах. Напомним, что порожденным подграфом называется подграф, максимальный на данном множестве вершин. Треугольник Т графа G называется нечетным, если в G имеется вершина, смежная с нечетным числом вершин в Т, и четным в противном случае.

Теорема. Следующие утверждения эквивалентны:

(1) G - реберный граф;

(2) ребра графа G можно разбить на полные подграфы таким образом, чтобы ни одна из вершин не принадлежала более чем двум подграфам;

(3) граф G не содержит звезду K1,s в качестве порожденного подграфа, и если два нечетных треугольника имеют общее ребро, то подграф, порожденный их вершинами, есть K4;

(4) ни один из девяти графов, приведенных на рисунке, не является порожденным подграфом графа G.

Доказательство. (1) влечет (2). Пусть G - реберный граф некоторого графа H. Не теряя общности, предположим, что в H нет изолированных вершин. Тогда ребра звезды каждой вершины графа Н порождают полный подграф графа G, и любое ребро графа G принадлежит только одному такому подграфу. Поскольку каждое ребро графа Н принадлежит звездам ровно двух вершин графа Н, то ни одна из вершин графа G не содержится более чем в двух таких подграфах.

(2) влечет (1). Пусть дано разбиение множества всех ребер графа G на полные подграфы S1, S2, • • •, Sn, удовлетворяющее утверждению (2). Покажем, как построить граф Н, для которого реберным графом будет граф G. Вершины графа Н соответствуют объединению множества S всех подграфов S1,S2,..., Sn и множества U вершин графа G, причем каждую вершину из U мы относим только к одному из подмножеств Si. Таким образом, объединение S È U является множеством вершин графа Н и две вершины смежны тогда и только тогда, когда соответствующие им множества имеют непустое пересечение, т. е. Н — граф пересечений Q(SÈU).

(2) влечет (4). Легко проверить, что ни один из девяти графов, приведенных на рисунке, не допускает разбиение множества ребер на полные подграфы, удовлетворяющее указанному выше условию. Окончательный результат вытекает из того, что каждый порожденный подграф реберного графа сам должен быть реберным графом.

(4) влечет (3). Покажем, что если граф G не удовлетворяет утверждению (3), то в G найдется порожденный подграф, изоморфный одному из девяти запрещенных графов. Предположим, что G содержит нечетные треугольники abc и abd, причем с и а не смежны.

В зависимости от того, существует или нет в графе G вершина v, смежная с нечетным числом вершин обоих треугольников, возможны два случая.

Случай 1. Пусть вершина v смежна с нечетным числом вершин треугольников abc и abd. Тогда имеются две возможности: или v смежна точно с одной вершиной в каждом треугольнике, или v

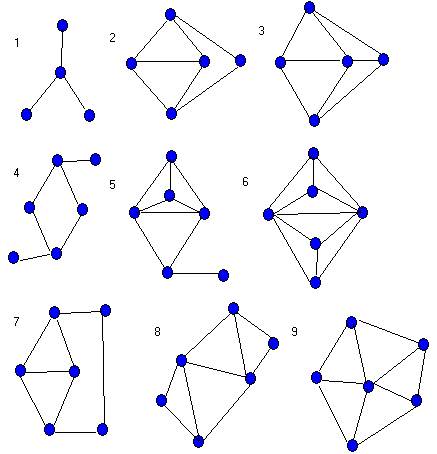
смежна с более чем одной вершиной в каждом треугольнике. Если выполняется последнее, то вершина v должна быть смежной со всеми четырьмя вершинами двух треугольников, и, следовательно, граф G содержит G3 (см. рис.) как порожденный подграф. При осуществлении первой возможности либо вершина v смежна только с одной из вершин а или b - и тогда получается граф G1, либо v смежна и с вершиной с, и с вершиной d — и тогда получается

граф G2.

Случай 2. Нет вершины, смежной с нечетным числом вершин каждого из этих двух треугольников. Пусть в этом случае вершины u и v смежны с нечетным числом вершин треугольников abc и abd соответственно. Здесь могут быть три подслучая:

Случай 2.1. Каждая вершина u и v смежна точно с одной вершиной

соответствующего треугольника.

Случай 2.2. Одна из вершин u и v смежна со всеми тремя вершинами «своего» треугольника, а другая только с одной.

Случай 2.3. Каждая вершина u и v смежна со всеми тремя вершинами соответствующего треугольника.

Прежде чем рассматривать эти подслучаи, отметим два факта. Если вершина u или v смежна с вершиной а или b, то она смежна также с вершиной с или d, так

как иначе в графе G был бы порожденный подграф G1. Далее, ни u, ни v не могут быть смежны одновременно с с и d, так как иначе в графе G был бы порожденный подграф G2 или G3.

Случай 2.1. Пусть uс, vdÎG. В зависимости от того, принадлежит или нет ребро uv графу G, получаем G4 или G5, в качестве порожденного подграфа. Если ub, vd Î G, то из предыдущих замечаний следует, что ud Î G, vc!ÎG; если uv!ÎG, то вершины {a, d, и, v} порождают G1, если же uvÎG, то вершины {а, b, с, d, и, v} порождают G8. Пусть ub, uaÎG; тогда обязательно ud, vcÎG. Поэтому, если uv!ÎG, то порождается граф G8, а если wuÎG, то граф G2. Наконец, если. ub, vbÎ G, то опять ud, vcÎG, откуда следует, что в зависимости от того,

принадлежит или нет ребро uv графу G, порожденным подграфом графа G будет G9 или G1.

Случай 2.2. Пусть uа, ub, uс Î G. Ясно, что если ud Î G, то G3— порожденный подграф графа G; таким образом, ud! ÎG. Далее, вершина v может быть смежной или с d, или с b. Если vd Î G, то в зависимости от того, принадлежит или нет ребро uv графу G, порожденным подграфом графа G будет G2 или G5. Если vbÎG,то порожденным подграфом графа G будет G3 или G1 в зависимости от того, смежна или нет вершина v с обеими вершинами с и u.

Случай 2.3. Если ud, vc или uv принадлежит G, то G3—порожденный подграф. Оставшаяся единственная возможность приводит к порожденному подграфу G6.

(3) влечет (1). Пусть для графа G справедливо утверждение (3). Можно считать граф G связным. Далее, должно выполняться точно одно из следующих двух условий:

1. Граф G содержит два четных треугольника, имеющих общее

ребро,

2. Если два треугольника графа G имеют общее ребро, то один

из них нечетный.

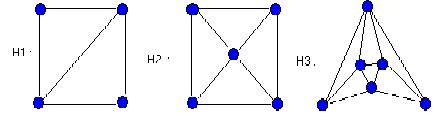
Можно показать, что если граф G удовлетворяет первому условию, то он совпадает с одним из графов H1=L(K1,3+x), Н2= L(H1) или H3=L(K4), изображенных на рисунке. Поэтому предположим, что G удовлетворяет второму условию. Приведем метод построения такого графа Н, что G=L(H).

Пусть F1— семейство всех клик графа G, не являющихся четными треугольниками, причем каждая такая клика рассматривается как множество вершин, и F3— семейство вершин графа G (которые берутся как отдельные элементы), принадлежащих некоторой клике

К семейства F1 и не смежных ни с одной вершиной графа G - К. Наконец, пусть F3— семейство ребер графа G (каждое ребро взято как множество, состоящее из двух вершин), принадлежащих одному и тому же четному треугольнику. Не трудно проверить, что граф G изоморфен реберному графу графа пересечений Н=Q (F1 U F2 UF3). Теорема доказана.

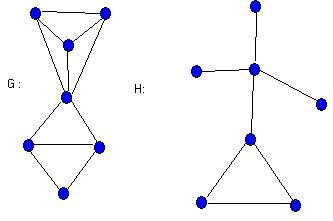
Последнее построение иллюстрируется на рисунке, где семействами данного графа G, определяющими граф пересечений Н, являются

F1 = {{1, 2, 3, 4}, {4, 5, 6}}, F2 = {{1}, {2}, {3}} и F3, = {{5,7}, {6,7}}; таким образом, G=L(H).