Специальные реберные графы

В этом разделе описываются реберные графы деревьев, полных графов и полных двудольных графов.

Следующий результат, полученный Чартрэндом, дает возможность определить, когда граф является реберным графом дерева.

Теорема. Граф есть реберный граф дерева тогда и только тогда, когда он является связным графом блоков, каждая точка сочленения которого принадлежит в точности двум блокам.

Доказательство. Предположим, что G=L(T) и Т - дерево. Тогда G- граф блоков В (Т), поскольку ребра и блоки в дереве совпадают. Каждая точка сочленения х графа G соответствует мосту uv дерева Т и принадлежит тем двум блокам графа G, которые соответствуют звездам вершин u и v. Необходимость доказана.

Установим достаточность. Пусть G - граф блоков, у которого каждая точка сочленения принадлежит ровно двум блокам. Так как любой блок графа блоков есть полный граф, то по теореме существует такой граф Н, что L(H)=G. Если G=К3, то можно взять H=K_1,3. Покажем, что для любого другого графа блоков G граф Н должен быть деревом. Доказываем от противного. Предположим, что Н не является деревом, т. е. содержит простой цикл. Если граф Н сам есть простой цикл, то по теореме L(H)=H, но единственный простой цикл, являющийся также графом блоков, есть К₃, а этот случай уже рассматривался. Следовательно, граф Н должен содержать как собственную часть простой цикл; другими словами, граф Н содержит простой цикл Z и ребро х, смежное с двумя ребрами цикла Z и не смежное с некоторым ребром у Î Z. Вершины х и у графа L (Н) лежат на простом цикле графа L (Н) и не смежны. Это противоречит тому, что L (Н) - граф блоков. Итак, Н - дерево. Теорема доказана.

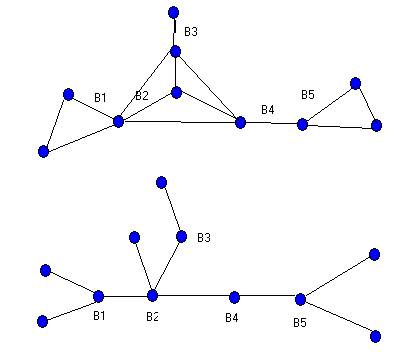
На рисунке показан граф блоков G, у которого каждая точка сочленения принадлежит точно двум блокам. Дерево Т, для которого G - реберный граф, строится следующим образом. Сначала образуется граф блоков B(G), а затем добавляются новые вершины в качестве вершин, не являющихся точками сочленения графа G, и ребра, соединяющие каждый блок с новыми вершинами.

Реберные графы полных и полных двудольных графов почти всегда характеризуются с помощью довольно простых утверждений, в которых говорится о смежности ребер в Кр и Km,n. Случай полных графов был независимо рассмотрен Чангом и Гоффманом.

Теорема. Если р!=8, то G — реберный граф графа К_Р тогда и только тогда, когда

1) G имеет (p,2) вершин,

2) С — регулярный граф степени 2(р—2),

3) любые две несмежные вершины одновременно смежны точно с четырьмя вершинами.

4) любые две смежные вершины одновременно смежны точно с р—2 вершинами.

Очевидно, что L (Кр) обладает этими свойствами. Но совсем не очевидно, что при р=8 существует ровно три графа, удовлетворяющих указанным условиям и не являющихся L(Кp).

Для полных двудольных графов соответствующий результат был получен Муном и Гоффманом.

Теорема. Если t!=4 и n!=4, то G -реберный граф графа Кt,n тогда и

только тогда, когда

1) G имеет tn вершин,

2) G -регулярный граф степени t+n-,

3) любые две несмежные вершины одновременно смежны точно с двумя вершинами.

4) среди смежных пар вершин точно n(m,2) пар одновременно смежны ровно с t -2 вершинами, а другие t (n,2) пар - ровно с п-2 вершинами.

При m=n=4 существует только один граф, удовлетворяющий этим условиям и не являющийся L(К_4,4). Он имеет 16 вершин, и был найден Шрихандом при доказательстве им теоремы в случае m = n.