Гомоморфизмы

В этом разделе мы для удобства будем рассматривать только связные графы. Элементарным гомоморфизмом графа G называется отождествление двух его несмежных вершин. Гомоморфизм графа G - это последовательность его элементарных гомоморфизмов.

Пусть G'— граф, который получается из графа G при гомоморфизме F. Тогда F можно рассматривать как функцию, отображающую V на V' такую, что если u и v смежны в G, то Fu и Fv смежны в G'. Заметим, что каждое ребро графа G' должно получаться из некоторого ребра графа G, т. е. если u' и v' смежны в G', то в G найдутся такие вершины u и v, что Fu = u' и Fv = v'.

Будем говорить, что

F- гомоморфизм графа G на граф G', а граф G'- гомоморфный образ графа G, и писать G'=FG. Так, в частности, каждый изоморфизм является гомоморфизмом. Простая цепь Р4 имеет четыре гомоморфных образа, которые изображены на рисунке.

Гомоморфизм F графа G называется полным порядка n, если

FG =Kn. Отметим, что каждый гомоморфизм F графа G на полный граф

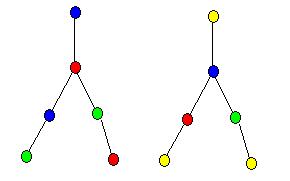
Кn соответствует n-раскраске графа G, поскольку вершины графа Кn можно рассматривать как цвета и по определению гомоморфизма ни одна пара вершин графа G с одинаковым цветом не смежна. Любая раскраска, определенная полным гомоморфизмом, обладает тем свойством, что для любых двух цветов в графе G найдутся смежные вершины г и v, окрашенные в эти цвета. В данном случае мы получаем полную раскраску. На рисунке показан граф с полными раскрасками порядков 3 и 4; Очевидно, что наименьший порядок всех полных гомоморфизмов графа G должен быть равным хr(G).

Теорема (Харари, Хедетниеми, Принс) обобщает более ранний результат Хайоша, который будет приведен как ее следствие.

Теорема. Для любого графа G и любого его элементарного гомоморфизма xr(G)<xr(eG)<l + xr(G).

Доказательство. Пусть e - элементарный гомоморфизм графа G, отождествляющий несмежные вершины u и v. Тогда любая раскраска графа eG порождает раскраску графа G, если u и v окрашены в один и тот же цвет; поэтому xr(G)<xr(eG). С другой стороны, раскраска графа eG получается из раскраски графа G, когда новой вершине приписывается цвет, отличный от всех цветов, используемых в раскраске G, так что хr(eG)<1 + хr(G)

Следствие (а). Для любого гомоморфизма F графа G

xr(G)<xr(FG).

Естественно теперь рассмотреть наибольший порядок всех полных гомоморфизмов графа G. Этот инвариант называется ахроматическим числом и обозначается Y(G). Поскольку G можно раскрасить р цветами, очевидно, что xr(G)< Y (G)<p. Ни одно из этих неравенств не дает хорошей оценки для Y;.

Теорема. Для любого графа G и любого его элементарного гомоморфизма

Y (G)—2<Y (eG)< Y (G).

Пример на рисунке показывает, что нижняя оценка достигается и, следовательно, она неулучшаема. Легко проверить, что Y (G)=5, в то время как Y (eG)=3.

Теорема, названная в работе Харари, Хедетниеми и Принса теоремой об интерполяции гомоморфизмов, сильно зависит от оценок.

Теорема. Для любого графа G и любого целого числа n, заключенного между xr(G) u Y(G), существует полный гомоморфизм (и, следовательно, полная раскраска) порядка n.

Теорема. Для любого графа G

Y+хr<p+1.

Следствие (а). Для любого графа G

Y<р—b0+1.