Однозначно раскрашиваемые графы

Пусть G — помеченный граф. Каждая его хr(G)-раскраска порождает разбиение множества его вершин на хr(G) одноцветных классов. Если xr(G) = n и каждая

n-раскраска графа G порождает одно и то же разбиение множества V, то G называется однозначно n-раскрашиваемым, или просто однозначно раскрашиваемым.

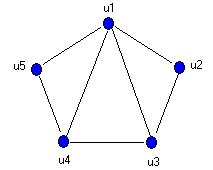
Граф, представленный на рисунке, однозначно 3-раскрашиваем, так как каждая его 3-раскраска дает разбиение {u1}, {u2, u4}, {и3, и5}. Пятиугольник не однозначно 3-раскрашиваем: возможны пять различных разбиений множества его вершин. Начнем с элементарных замечаний, касающихся однозначно раскрашиваемых графов. Прежде всего, в любой n-раскраске однозначно n-раскрашиваемого графа G каждая вершина v смежна, по крайней мере с одной вершиной каждого цвета, отличного от цвета, приписанного v. Иначе можно было бы получить другую n-раскраску графа G, перекрасив вершину v. Отсюда следует, что d(G)>n -1. Необходимое условие однозначной раскрашиваемости графа найдено Картрайтом и Харари.

Теорема. В n-раскраске однозначно n-раскрашиваемого графа подграф, порожденный объединением любых двух одноцветных классов, связен.

Из теоремы следует, что каждый однозначно n-раскрашиваемый граф связен. Чартрэнд и Геллер получили более сильный результат:

Теорема. Каждый однозначно n-раскрашиваемый граф (n - 1)-связен.

Поскольку объединение любых k одноцветных классов однозначно

n-раскрашиваемого графа, 2>n, порождает однозначно n-раскрашиваемый граф, то из теоремы вытекает

Следствие (а). В каждой n-раскраске однозначно n-раскрашиваемого графа подграф, порожденный объединением любых k одноцветных классов,

2<k<n, (k - 1) -связен.

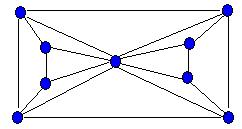
Легко привести примеры 3-хроматических графов, не содержащих треугольников. Действительно, в теореме говорится, что для любого n существуют n-хроматические графы, не содержащие треугольников и, следовательно, не имеющие подграфов, изоморфных Кn. Харари, Хедетниеми и Робинсон получили более сильный результат:

Теорема. Для каждого n>3 существует однозначно

n-раскрашиваемый граф, не содержащий подграфов, изоморфных Кn.

Граф G, приведенный на рисунке, иллюстрирует теорему для случая n=3.

Естественно, граф однозначно 1-раскрашиваем тогда и только тогда, когда он

1-раскрашиваем, т. е. вполне несвязен. Хорошо известно, что граф G однозначно 2-раскрашиваем тогда и только тогда, когда он 2-хроматический и связный.

Как и можно было ожидать, об однозначно n-раскрашиваемых графах, n>З, известно мало. Для планарных графов сведений больше, но в силу теоремы о пяти красках достаточно рассматривать только значения 3<n<5. Результаты в этом направлении принадлежат Чартрэнду и Геллеру.

Теорема. Пусть G есть 3-хроматичвский плоский граф. Если G содержит такой треугольник Т, что для любой вершины v графа G существует последовательность Т1,Т2,Т3,...., Тt треугольников, в которой соседние

два имеют общее ребро и v Î Тt, то G — однозначно 3-раскрашиваемый граф.

Из этой теоремы немедленно вытекает

Следствие (а). Если двусвязный 3-хроматический плоский граф G имеет не более одной области, не являющейся треугольником, то G — однозначно 3-раскрашиваемый граф.

Предложение, обратное следствию (а), не верно: однозначно

3-раскрашиваемый пленарный граф может иметь более одной области, не являющейся треугольником (рис.). Однако каждый однозначно

3-раскрашиваемый пленарный граф должен содержать треугольники.

Теорема. Однозначно 3-раскрашиваемый планарный граф,

имеющий не менее 4 вершин, содержит, по крайней мере два треугольника.

В случае однозначно 4-раскрашиваемых пленарных графов ситуация особенно проста.

Теорема. Каждый однозначно 4-раскрашиваемый планарный граф является максимальным планарным графом.

Хотя вопрос существования 5-раскрашиваемых пленарных графов остается все еще открытым, результат Хедетниеми, приведенный в работе Чартрэнда и Геллера, разрешает проблему однозначно 5-раскрашиваемости.

Теорема. Ни один из планарных графов не является однозначно 5-раскрашиваемым.