Виды трендов

Построение модели тенденции (уравнения тренда) включает в себя следующие этапы работы:

- выбор математической функции, описывающей тенденции;

- оценка или определение параметров модели;

- проверка адекватности выбранной функции и оценка точности модели;

- расчет точечного и интервального прогнозов.

По аналитическому виду различают следующие виды трендов.

Линейный тренд ,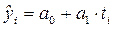

где 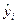- выровненные (теоретические) уровни тренда;

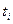- номера моментов или периодов времени, к которым относятся уровни временного ряда;

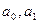- параметры уравнения тренда.

Величина параметров определяется с помощью МНК. Для этого строят систему нормальных уравнений:

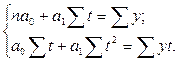
Линейный тип тренда подходит для отображения тенденции примерно равномерного изменения уровней, т.е. равных абсолютных приростов.

Основные свойства линейного тренда:

1) равные изменения за равные промежутки времени;

2) если средний абсолютный прирост – положительная величина, то величина относительного прироста постепенно уменьшается;

3) если среднее абсолютное изменение – отрицательная величина, то относительные изменения по абсолютной величине увеличиваются.

Параболический тренд .

Данная функция рекомендуется для моделирования тенденции, если временной ряд характеризуется постоянным абсолютным ускорением, т.е. постоянными являются вторые разности (приросты абсолютных приростов).

t		Абсолютные приросты (скорость)	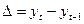Приросты абсолютных приростов (ускорение)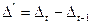
		-	-
			-

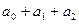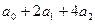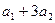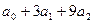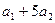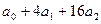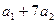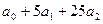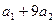Широкое применение среди функций с монотонным характером возрастания (убывания) и отсутствием пределов роста (снижения) имеет показательная функция: .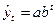

Она выбирается, когда ряд динамики характеризуется стабильными (постоянными) коэффициентами роста:

t
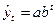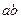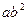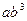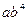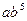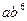Кр	-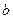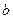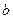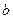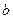

Рост по показательной функции означает геометрическую прогрессию уровней динамического ряда, что в экономике возможно сравнительно небольшой период времени.

Предполагая разную меру пропорциональности изменений уровней во времени, может быть использована степенная функция: :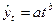

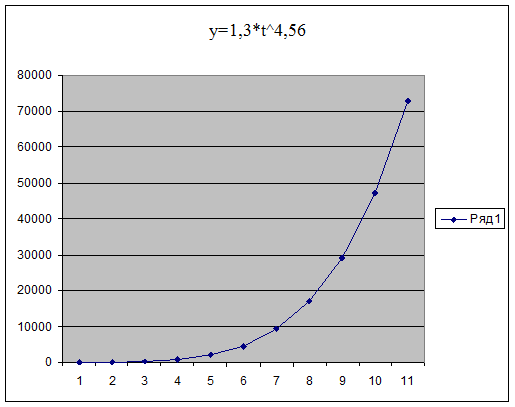
При 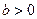степенная функция характеризует непрерывный рост уровней с падающими темпами роста, а при 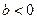- их ускоренное снижение:

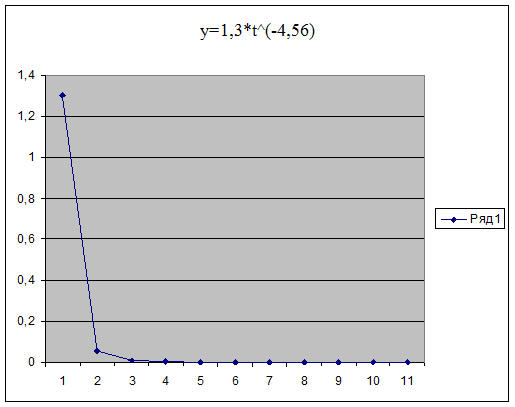
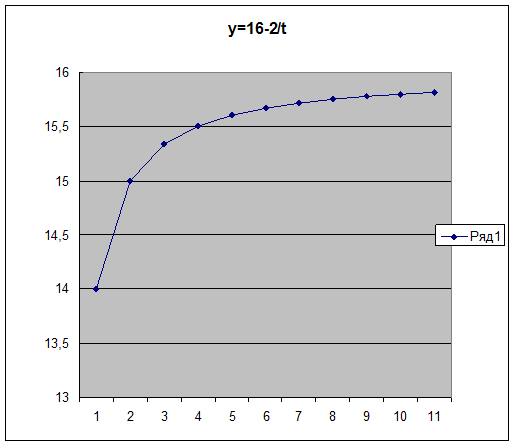
Гиперболический тренд .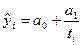

Содержание параметров гиперболы:

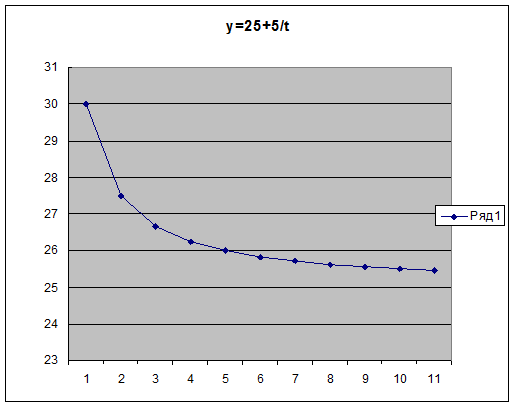
а₀ – предел, к которому стремится уровень ряда.

а₁ – основной параметр гиперболы, если а₁>0, то уровни ряда замедленно снижаются и стремятся к а₀, если а₁<0, то уровни ряда замедленно возрастают и стремятся к а₀.

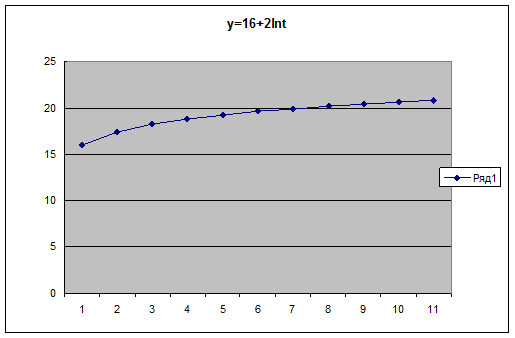
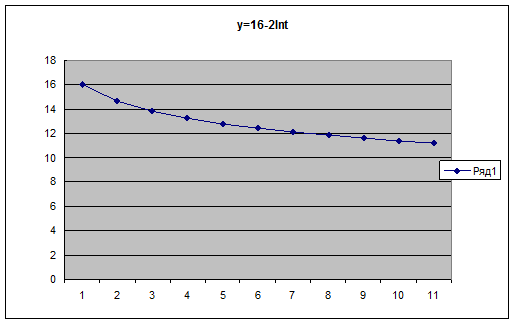
Логарифмический тренд 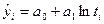применяют также как и гиперболический, если необходимо отразить постепенно затухающий процесс. Однако эти тренды имею существенное различие. Затухание по гиперболе происходит быстро при приближении к конечному пределу, а при логарифмическом тренде затухающий процесс продолжается без ограничения и гораздо медленнее.

Если а₁>0, то уровни возрастают с замедлением, если а₁<0, то уровни уменьшаются, тоже с замедлением.