Момент инерции тела относительно производной оси О равен сумме моментов инерции этого же тела относительно оси, проходящей через центр масс и произведения массы тела на квадрат расстояния между осями.
Теорема Штейнера.
Имеется тело массой М, разбиваем его на N частей массой 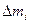 - каждая. Имеется 2 оси О и О/. Вычислим момент инерции относительно оси О.
- каждая. Имеется 2 оси О и О/. Вычислим момент инерции относительно оси О.
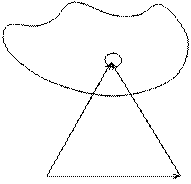
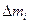
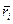
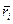
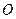
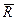
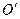
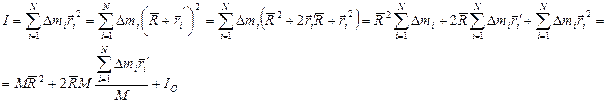 пусть ось
пусть ось  проходит через центр масс и тогда
проходит через центр масс и тогда 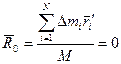
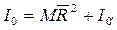 - теорема Штейнера
- теорема Штейнера
Рассмотрим вращающееся вокруг оси Z твердое тело. Выделим массу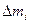 ;
; 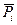 - импульс i-той части тела;
- импульс i-той части тела; 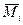 - момент импульса i-той части
- момент импульса i-той части
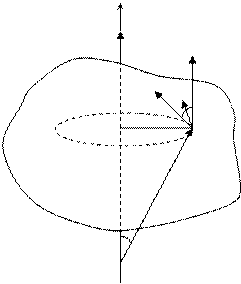
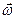 .
.
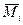
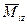
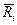
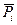
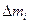
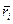
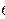
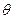
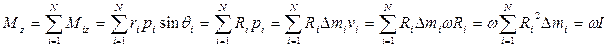
Для тела вращающегося вокруг оси симметрии 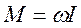
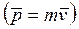
Дифференцируем левую и правую часть этого соотношения по t.
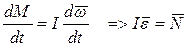
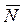 - результирующий момент сил, действующий на тело.
- результирующий момент сил, действующий на тело.
Данное соотношение является основным уравнением динамики вращающегося движения твердого тела и является аналогом 2-ого закона Ньютона
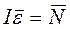
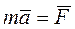
| Поступательное движение | Вращательное движение |
| m | I |
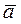
| 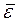
|
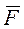
| 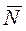
|
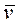
| 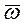
|
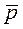
| 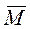
|
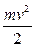
| 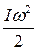
|
 2014-02-02
2014-02-02 366
366








