2014-02-02
855
Универсальная функция Кирхгофа связана с равновесной спектральной плотностью энергии теплового излучения простым соотношением:
,
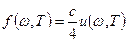где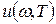 
-плотность энергии, приходящаяся на единичный интервал частот.
Все попытки получения в рамках классической физики функции 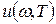, вид которой был бы в согласии с экспериментальными данными, не увенчались успехом. Предположим, что у нас имеется полость, заполненная равновесным излучением, представляющим собой совокупность стоячих волн. Расчеты показывают, что число стоячих волн, приходящихся на диапазон частот 
:
.
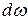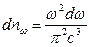Согласно классическому принципу равнораспределения энергии по степеням свободы на каждую стоячую электромагнитную волну в полости должна приходиться энергия равная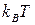 
(
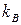- постоянная Больцмана). Из нее 
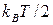приходится на электрическую энергию волны и 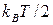на магнитную энергию. Тогда для плотности энергии, приходящейся на интервал частот 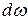можем записать:
.
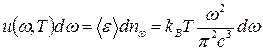Находим:
.
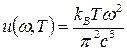Для испускательной способности абсолютно черного тела находим:
.
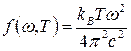Соотношение называют формулой Рэлея – Джинса. хорошо согласуется с экспериментальными данными только в области малых частот. В области высоких частот, как показывает эксперимент,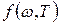
экспоненциально убывает.
Для нахождения плотности энергии равновесного излучения в полости необходимо проинтегрировать функцию 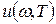по частоте от 0 до 
:
.
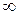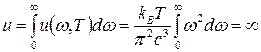Легко видеть, что интегрирование в соотношении приводит к бесконечной плотности энергии в полости, что конечно не согласуется с экспериментальными данными. Данный результат в физике получил название «ультрафиолетовой катастрофы», т.к. интеграл в (10) разошелся на верхнем пределе, т.е. в области высоких частот. Разрешить данное противоречие в рамках классической физики не удалось.
