Запас устойчивости по алгебраическому критерию Гурвица
 ,
, 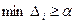 , где
, где 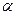 - запас устойчивости.
- запас устойчивости.
Запасом устойчивости считается некоторая величина 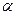 , при которой самый min определитель Гурвица не должен быть меньше этой величины.
, при которой самый min определитель Гурвица не должен быть меньше этой величины.
При частотных критериях устойчивости различают два критерия: по амплитуде и по фазе. Запас устойчивости по амплитуде определяется наиближайшей точкой по отношению к критической. В численном значении - это длина отрезка [0;B], где В – точка пересечения годографа системы и отрицательной оси.
Нормированная величина запаса устойчивости:

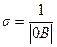 - запас устойчивости по модулю.
- запас устойчивости по модулю.
Если 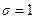 , то система находится на границе устойчивости;
, то система находится на границе устойчивости;
Если 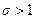 , то система устойчивая;
, то система устойчивая;
Если 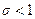 - система неустойчива.
- система неустойчива.
На практике считается допустимым запас по амплитуде в логарифмическом масштабе - 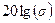 , что составляет
, что составляет 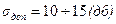 .
.
Чтобы определить, обладает ли САУ заданным запасом устойчивости по амплитуде, проводится следующие исследования:
1. Строится годограф амплитудно-фазовой характеристики разомкнутой системы.
2. Определяется ближайшая точка пересечения данного годографа с действительной осью по отношению к точке [-1,0].
3. Определяется запас устойчивости по формуле: 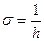 , где h – это отрезок [0;B].
, где h – это отрезок [0;B].
4. Если полученный запас устойчивости больше заданного, то САУ отвечает заданному запасу устойчивости, в противном случае САУ не обладает заданным запасом.
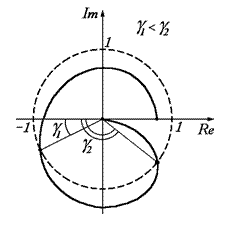 Запасом устойчивости по фазе называется минимальный угол, образуемый отрицательной действительной осью и прямой, соединяющий начало координат и точку пересечения годографа амплитудно-фазовой характеристики разомкнутой системы и окружности с единичным радиусом с центром в начале координат.
Запасом устойчивости по фазе называется минимальный угол, образуемый отрицательной действительной осью и прямой, соединяющий начало координат и точку пересечения годографа амплитудно-фазовой характеристики разомкнутой системы и окружности с единичным радиусом с центром в начале координат.
На практике допустимым запасом устойчивости считается угол: 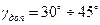 .
.
Если 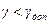 , то система не обладает запасом устойчивости;
, то система не обладает запасом устойчивости;
Если 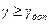 , то система обладает запасом устойчивости.
, то система обладает запасом устойчивости.
 2014-02-02
2014-02-02 651
651








