Ритмические процессы любой природы, характеризующиеся повторяемостью во времени, называются колебаниями.
Колебание – процесс, характеризующийся повторяемостью во времени параметров, его описывающих. Единство закономерностей ритмических процессов позволило разработать единый математический аппарат для их описания – теорию колебаний. Существуют множество признаков, по которым могут быть классифицированы колебания.
По физической природе колеблющейся системы различают механические и электромагнитные колебания.
Колебания называются периодическими, если величина, характеризующая состояние системы, повторяется через равные промежутки времени – период колебания.
Период (T) - минимальное время, через которое повторяется состояние колебательной системы, т.е. время одного полного колебания.
Для таких колебаний
x(t)=x(t+T);(3.1)
Периодическими являются колебания маятника часов, переменный ток, биение сердца, а колебания деревьев под порывом ветра, курсов иностранных валют – не периодические.
Кроме периода в случае периодических колебаний определена их частота.
Частота (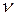 )т.е. число колебаний в единицу времени.
)т.е. число колебаний в единицу времени.
Частота -величина, обратная периоду колебания,
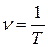 ; (3.2)
; (3.2)
Единицей измерения частоты является Герц: 1 Гц = 1 с-1, частота соответствующая одному колебанию в секунду. При описании периодических колебаний также используется циклическая частота – число колебаний за 2 π секунд:
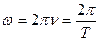 ; (3.3)
; (3.3)
При периодических колебаниях эти параметры постоянны, а при других колебаниях могут изменяться.
Закон колебаний – зависимость колеблющейся величины от времени x(t) - может быть может быть разной. Наиболее простыми являются гармонические колебания (рис3.1), для которых колеблющаяся величина меняется по закону синуса или косинуса, что позволяет использовать одну функцию для описания процесса во времени:
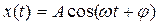 ;
;
или (3.4)
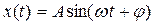 ;
;
Здесь: x (t) – значение колеблющейся величины в данный момент времени t, А – амплитуда – наибольшее отклонение колеблющейся величины от среднего значения., ω – циклическая частота, (ωt+φ) – фаза колебания, φ – начальная фаза.
Гармоническому закону подчиняются многие известные колебательные процессы. в т.ч. упомянутые выше, но наиболее существенно что с помощью метода Фурье любая периодическая функция раскладывающаяся на гармонические составляющие (гармоники) с кратными частотами:
f (t)= А 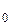 + А 1cos(
+ А 1cos(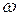 t +
t +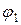 )+ А
)+ А 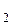 cos (2
cos (2 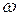 t+
t+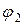 )+…; (3.5)
)+…; (3.5)
Здесь основная частота определяется периодом процесса: 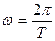 .
.
Каждая гармоника характеризуется частотой ( ) и амплитудой (А). Совокупность гармоник называется с пектром. Спектры периодических колебаний дискретные (линейчатые) (рис.3.1а), а не периодических непрерывные (рис.3.1б).
) и амплитудой (А). Совокупность гармоник называется с пектром. Спектры периодических колебаний дискретные (линейчатые) (рис.3.1а), а не периодических непрерывные (рис.3.1б).
А А
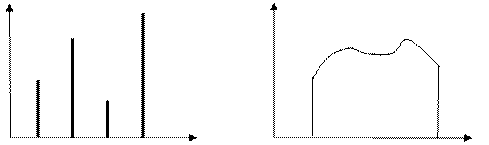
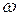
Рис. 3.1 Дискретные (а) и непрерывные (б) спектры сложных колебательных
 2014-02-02
2014-02-02 2042
2042
