2014-02-02
2173
В ряде процедур классификации (кластер-процедур) используют понятия расстояния между группами объектов и меры близости двух групп объектов.
Пусть Si - i- я группа (класс, кластер), состоящая из ni объектов;
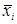- среднее арифметическое векторных наблюдений Si группы, т.е. «центр тяжести» i- ой группы;
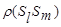-расстояние между группами Sl и Sm..
Наиболее употребительными расстояниями и мерами близости между объектов являются:
─ расстояние, измеряемое по принципу «ближайшего соседа»
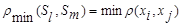(7.5)
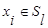
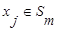
─ расстояние, измеряемое по принципу «дальнего соседа»
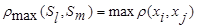(7.6)
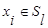
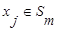
─ расстояние, измеряемое по «центрам тяжести» групп
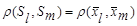(7.7)
─ расстояние, измеряемое по принципу «средней связи». Это расстояние определяется как среднее арифметическое всех парных расстояний между представителями рассматриваемых групп
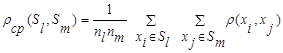(7.8)
Академиком А.Н.Колмогоровым было предположено «обобщенное расстояние» между классами, которое в качестве частных случаев включает в себя все рассмотренные выше виды расстояний.
Обобщенное расстояние основано на понятии так называемого «обобщенного среднего», а точнее – степенного среднего и определяется формулой:
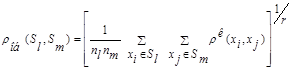(7.9)
Можно показать, что при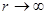 
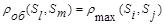
при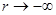 
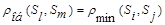
при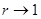 
.
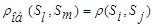Из формулы (7.9) следует, что если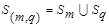 
-группа элементов, полученная путем объединения кластеров 
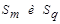, то обобщенное расстояние между кластерам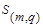и 
и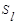 
определяется по формуле
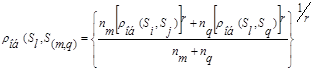(7.10)
Расстояние между группами элементов особенно важно в так называемых агломеративных иерархических кластер – процедурах, так как принцип работы таких алгоритмов состоит в последовательном объединении сначала самых близких элементов, а затем и целых групп все более и более отдаленных друг от друга элементов.
При этом расстояние между классам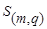и 
и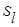 
, являющимся объединением двух других классов 
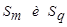, можно определить по формуле:
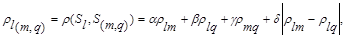(7.11)
где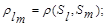 
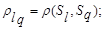
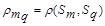- расстояние между классами 
;
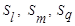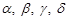-числовые коэффициенты, значение которых определяет специфику процедуры, ее алгоритм.
Например, пр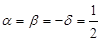и 
и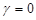 
приходим к расстоянию, построенному по принципу «ближайшего соседа». Пр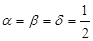и 
и 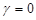расстояние между классами определяется по принципу «дальнего соседа», как расстояние между двумя самыми дальними элементами этих классов. И наконец, при
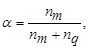
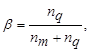
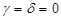
Соотношение (7.11) приводит к расстоянию ρ между классами, вычисленному как среднее из расстояния между всеми парами элементов, один из которых берется из одного класса, а другой – из другого класса.
