Метод определения минимально-безопасного расстояния
Введем некоторые определения, которые потребуются в дальнейшем.
Определение 1. Будем говорить, что столкновение автомобилей  и
и  на отрезке времени
на отрезке времени  не произойдет, а отрезок времени
не произойдет, а отрезок времени  будем называть безопасным (в смысле невозможности столкновения), если для любого
будем называть безопасным (в смысле невозможности столкновения), если для любого 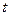 из этого отрезка выполняется неравенство (2.1.15).
из этого отрезка выполняется неравенство (2.1.15).
Определение 2. Момент времени 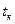 будем называть моментом касания автомобилей
будем называть моментом касания автомобилей  и
и  на отрезке времени
на отрезке времени  , если
, если 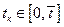 и выполняется равенство
и выполняется равенство
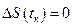 .
.
Определение 3. Момент касания 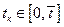 будем называть опасным моментом касания, или моментом столкновения автомобилей
будем называть опасным моментом касания, или моментом столкновения автомобилей  и
и  на отрезке времени
на отрезке времени  , если выполняется условия:
, если выполняется условия: 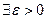 :
:
1) 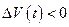 при
при 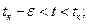
2)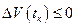 ; (2.2.1)
; (2.2.1)
3)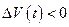 при
при 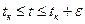 .
.
Механический смысл неравенства (2.2.1) состоит в том, что после момента касания начинает происходить деформация элементов кузова автомобилей, поэтому расстояние между центрами масс автомобилей  и
и  начинает уменьшаться.
начинает уменьшаться.
Определение 4. Момент касания 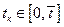 будем называть безопасным моментом касания автомобилей
будем называть безопасным моментом касания автомобилей  и
и  на отрезке времени
на отрезке времени  , если выполняются условия:
, если выполняются условия: 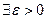 :
:
1) 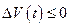 при
при 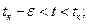
2)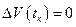 ; (2.2.2)
; (2.2.2)
3)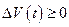 при
при 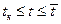 .
.
Механический смысл этого определения состоит в том, что автомобиль  , догнав и коснувшись передней кромкой переднего бампера задней кромки заднего бампера автомобиля
, догнав и коснувшись передней кромкой переднего бампера задней кромки заднего бампера автомобиля  в момент времени
в момент времени 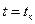 , или начнет двигаться с той же скоростью, что и автомобиль
, или начнет двигаться с той же скоростью, что и автомобиль  , или начнет отставать от автомобиля
, или начнет отставать от автомобиля  .
.
Отметим, что условия (2.2.2) совпадают с необходимым условием минимума функции 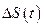 на отрезке времени
на отрезке времени  в момент времени
в момент времени 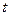 =
=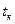 .
.
Определение 5. Выбранное начальное расстояние 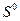 будем называть безопасным на отрезке времени
будем называть безопасным на отрезке времени  для автомобилей
для автомобилей  и
и  , если неравенство (2.1.15) выполняется для всех моментов времени
, если неравенство (2.1.15) выполняется для всех моментов времени 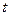 из отрезка
из отрезка  .
.
Безопасное начальное расстояние 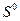 , вообще говоря, является функционалом от параметров движения автомобилей
, вообще говоря, является функционалом от параметров движения автомобилей  и
и  , т. е. зависит от ускорений автомобилей
, т. е. зависит от ускорений автомобилей 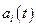
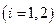 на отрезке времени
на отрезке времени  , начальных скоростей
, начальных скоростей 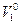 и
и 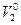 , технического состояния, дорожных условий и т.д. Следует отметить, что если для заданного движения автомобилей мы нашли некоторое безопасное расстояние
, технического состояния, дорожных условий и т.д. Следует отметить, что если для заданного движения автомобилей мы нашли некоторое безопасное расстояние 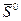 , то любое расстояние
, то любое расстояние 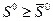 будет тоже безопасным. Так как множество безопасных расстояний S0=
будет тоже безопасным. Так как множество безопасных расстояний S0=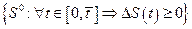 длярассматриваемых движений автомобилей
длярассматриваемых движений автомобилей  и
и  ограничено снизу нулем, то существует точная нижняя граница этого множества
ограничено снизу нулем, то существует точная нижняя граница этого множества
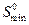 =
=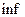 S0
S0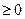 (2.2.3)
(2.2.3)
такая, что любое 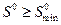 является безопасным начальным расстоянием для заданных движений автомобилей
является безопасным начальным расстоянием для заданных движений автомобилей  и
и  , а для любого
, а для любого 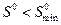 автомобили
автомобили  и
и  неизбежно столкнутся.
неизбежно столкнутся.
Определение 6. Наименьшее значение из множества S0, определенное равенством (2.2.3), будем называть минимально-безопасным начальным расстоянием и обозначать 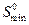 .
.
Если при движении автомобилей  и
и  водителю автомобиля
водителю автомобиля  , который находился в начальный момент времени
, который находился в начальный момент времени 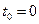 на расстоянии
на расстоянии 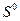 от автомобиля
от автомобиля  , удается добиться того, что функция
, удается добиться того, что функция 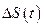 принимает на отрезке времени
принимает на отрезке времени  неотрицательные значения, т. е. выполняется неравенство (2.1.15), то в этом случае из равенства (2.1.13) следует, что
неотрицательные значения, т. е. выполняется неравенство (2.1.15), то в этом случае из равенства (2.1.13) следует, что
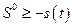 (2.2.4)
(2.2.4)
на рассматриваемом отрезке времени. Неравенство (2.2.4) означает согласно определению 1, что столкновение автомобилей  и
и  на этом отрезке времени не произойдет. Если же водителю автомобиля
на этом отрезке времени не произойдет. Если же водителю автомобиля  не удается добиться (вплоть до применения экстренного торможения) выполнения неравенства (2.2.4) в любой момент времени на отрезке
не удается добиться (вплоть до применения экстренного торможения) выполнения неравенства (2.2.4) в любой момент времени на отрезке  , то столкновение автомобилей
, то столкновение автомобилей  и
и  необходимо произойдет. Это означает, что он неправильно выбрал начальное расстояние
необходимо произойдет. Это означает, что он неправильно выбрал начальное расстояние 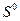 в начальный момент времени
в начальный момент времени 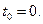
Утверждение 1. Если при движении автомобилей  и
и  функция
функция 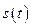 принимает неотрицательные значения на отрезке времени
принимает неотрицательные значения на отрезке времени  , то столкновение автомобилей
, то столкновение автомобилей  и
и  на этом отрезке времени не произойдет, а начальное безопасное расстояние
на этом отрезке времени не произойдет, а начальное безопасное расстояние 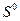 может быть любым неотрицательным числом, т. е. минимально-безопасное расстояние
может быть любым неотрицательным числом, т. е. минимально-безопасное расстояние 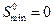 .
.
Доказательство. Действительно, так как 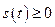 для
для 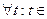
 , то в силу равенства (2.1.13) функция
, то в силу равенства (2.1.13) функция 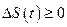 и, следовательно, согласно определению 1 столкновение автомобилей
и, следовательно, согласно определению 1 столкновение автомобилей  и
и не произойдет.
не произойдет.
В этом случае начальное расстояние между автомобилями может быть любым 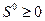 , следовательно,
, следовательно, 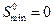 .
.
Пусть движение автомобилей  и
и  таково, что функция
таково, что функция 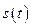 принимает на отрезке времени
принимает на отрезке времени  как неотрицательные, так и отрицательные значения.
как неотрицательные, так и отрицательные значения.
Утверждение 2. Если функция 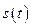 принимает на отрезке времени
принимает на отрезке времени  как отрицательные, так и неотрицательные значения, то минимально-безопасное расстояние для этого отрезка времени определяется равенством
как отрицательные, так и неотрицательные значения, то минимально-безопасное расстояние для этого отрезка времени определяется равенством
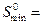
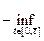
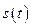 (2.2.5)
(2.2.5)
Доказательство: Так как функция 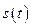 , определенная равенством (2.1.14), непрерывна и дифференцируема на отрезке времени
, определенная равенством (2.1.14), непрерывна и дифференцируема на отрезке времени  , то она необходимо ограничена и достигает своей точной нижней границы при некотором значении
, то она необходимо ограничена и достигает своей точной нижней границы при некотором значении 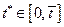 , т. е.
, т. е.
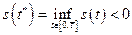 , (2.2.6)
, (2.2.6)
так как функция принимает и отрицательные значения на рассматриваемом отрезке. Покажем, что величина 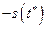 является минимально-безопасным начальным расстоянием на отрезке
является минимально-безопасным начальным расстоянием на отрезке  . Подставляя в равенстве (3.1.13) вместо
. Подставляя в равенстве (3.1.13) вместо 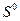 значение функции
значение функции 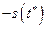 , получим
, получим
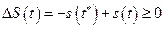
для 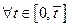 , так как из определения точной нижней границы следует
, так как из определения точной нижней границы следует
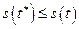 для
для 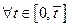 .
.
Таким образом, получили, что начальное расстояние 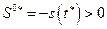 является безопасным. Покажем, что оно является минимально-безопасным начальным расстоянием для отрезка времени
является безопасным. Покажем, что оно является минимально-безопасным начальным расстоянием для отрезка времени  .
.
Допустим противное. Пусть существует безопасное 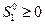 :
: 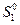 <
<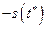 и
и
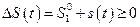 (2.2.7)
(2.2.7)
для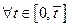 . Возьмем произвольное число
. Возьмем произвольное число 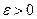 , удовлетворяющее неравенству
, удовлетворяющее неравенству
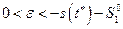
или
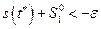 .
.
Из равенства (2.2.6) и свойств точной нижней границы для выбранного 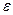 >0 найдется
>0 найдется
 ,
,
но тогда
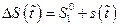 <
<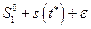 <
<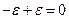 ,
,
т.е. 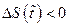 , что противоречит нашему предположению о том, что
, что противоречит нашему предположению о том, что 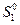 является безопасным расстоянием, т.е. неравенству (2.2.7). Полученное противоречие и доказывает наше утверждение.
является безопасным расстоянием, т.е. неравенству (2.2.7). Полученное противоречие и доказывает наше утверждение.
Доказанные утверждения дают практический метод нахождения минимально-безопасного начального расстояния между автомобилями  и
и  для заданного отрезка времени.
для заданного отрезка времени.
При экстренном торможении автомобиля  для нахождения минимально-безопасного расстояния
для нахождения минимально-безопасного расстояния 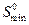 в качестве отрезка времени
в качестве отрезка времени  необходимо рассматривать отрезок времени
необходимо рассматривать отрезок времени 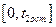 , где
, где 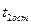
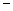 время движения автомобиля
время движения автомобиля  до полной остановки.
до полной остановки.
Таким образом, для нахождения минимально-безопасного расстояния 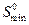 в случае, если функция
в случае, если функция 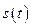 может принимать на отрезке времени
может принимать на отрезке времени 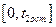 как положительные, так и отрицательные значения, необходимо:
как положительные, так и отрицательные значения, необходимо:
1) найти все моменты времени 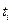 подозрительные на экстремум, т.е. точки, в которых выполняется равенство
подозрительные на экстремум, т.е. точки, в которых выполняется равенство
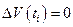 ;
;
3) найти все точки 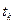
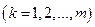 (безопасные моменты касания), в которых функция
(безопасные моменты касания), в которых функция 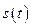 достигает отрицательного минимума, тогда минимально-безопасное расстояние определяется равенством
достигает отрицательного минимума, тогда минимально-безопасное расстояние определяется равенством
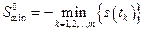 ,
,
если 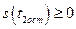 , и
, и
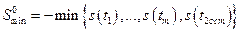 ,
,
если 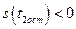 .
.
Если функция 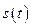 принимает только положительные значения, т.е.
принимает только положительные значения, т.е. 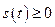 для всех
для всех 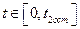 , то в этом случае
, то в этом случае 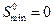 .
.
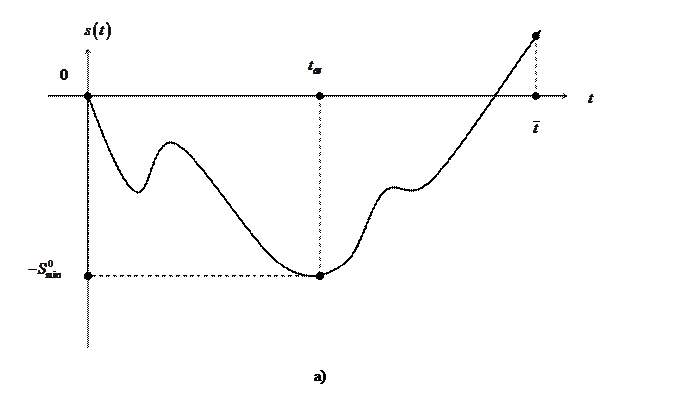
Геометрический смысл нахождения минимально-безопасного расстояния состоит в нахождении положительной величины 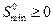 (рис.2.2.1, а), б)), на
(рис.2.2.1, а), б)), на
которую необходимо сдвинуть график функции 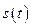 вдоль оси
вдоль оси 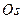 вверх, чтобы график функции
вверх, чтобы график функции 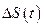 только касался оси
только касался оси 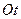 и полностью лежал бы в первом
и полностью лежал бы в первом
квадранте системы координат 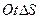 при
при 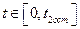 .
.
Метод, основанный на доказанных утверждениях, позволяет в дальнейшем находить минимально-безопасное расстояние между автомобилями, дви-
 | |||
 | |||


Рис.2.2.1
жущимися в попутном направлении, при любом техническом состоянии автомобилей  ,
, и любых дорожных условиях.
и любых дорожных условиях.
 2014-01-24
2014-01-24 726
726








