ВОПРОС 5.
1. Глава 51 УПК РФ.
2. Закон РФ от 02.07.1992 г. № 3185-1 (ред. от 27.07.2010) «О психиатрической помощи и гарантиях прав граждан при ее оказании»
3. Постановление Конституционного Суда РФ от 20.11.2007 г. № 13-П «По делу о проверке конституционности ряда положений статей 402, 433, 437, 438, 439, 441, 444 и 445 Уголовно-процессуального кодекса Российской Федерации в связи с жалобами граждан С.Г. Абламского, О.Б. Лобашовой и В.К. Матвеева»
Данный этап окончания ПС по своему содержанию в основном аналогичен тому, который сопряженс составлением обвинительного заключения (акта).
Ч. 3 ст. 439 УПК предусматривает ограниченный круг лиц, которым предоставлено право знакомиться с материалами УД, – это защитник, законные представители лица, совершившего общественно опасное деяние, и потерпевший. Однако данная норма признана не соответствующей Конституции РФ в той мере, в какой она не позволяет лицам, в отношении которых осуществляется производство о применении ПММХ, лично знакомиться с материалами уголовного дела, участвовать в судебном заседании при его рассмотрении, заявлять ходатайства, инициировать рассмотрение вопроса об изменении и прекращении применения указанных мер и обжаловать принятые по делу процессуальные решения (см. указанное Постановление КС).
По окончании ПС обвинительное заключение не составляется, а выносится постановление, содержание которого почти аналогично обвинительному заключению (ч. 4 ст. 439 УПК). Постановление должно быть утверждено прокурором. Копия постановления вручается защитнику и законному представителю (ч.6 ст. 439 УПК), а также самому лицу, в отношении которого применяются ПММХ (см. указанное Постановление КС).
В разделах дифференциального и интегрального исчислений мы имеем дело с функциями одного переменного. На практике часто приходится иметь дело с функциями двух, трех и большего числа переменных. Такие функции называются функциями многих переменных. Примером такой функции является производственная функция Кобба-Дугласа
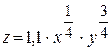
где 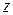 есть величина выпуска продукции, а
есть величина выпуска продукции, а 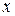 и
и 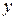 обозначают объемы затраченных ресурсов труда и капитала соответственно.
обозначают объемы затраченных ресурсов труда и капитала соответственно.
Приведем еще примеры функций 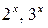 и
и 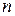 переменных:
переменных:
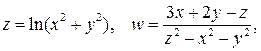
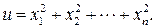
2. 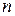 -мерное пространство Rn
-мерное пространство Rn 
Определение. Пусть 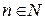 . Будем называть R n следующее множество упорядоченных наборов действительных чисел:
. Будем называть R n следующее множество упорядоченных наборов действительных чисел:
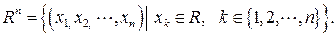
Сами упорядоченные наборы 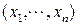 будем называть точками
будем называть точками  , а числа
, а числа 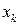 , где
, где 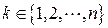 , будем называть координатами этой точки.
, будем называть координатами этой точки.
Часто для удобства точки Rn будем обозначать так: 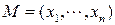 или
или 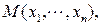 или
или 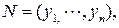 или
или 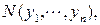 и т. д.
и т. д.
В пространстве Rn вводится расстояние между точками 
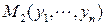 по формуле
по формуле
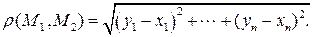 (1)
(1)
Замечание. При 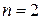 и
и 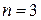 равенство (1) представляет известные формулы расстояния между точками на плоскости и в пространстве.
равенство (1) представляет известные формулы расстояния между точками на плоскости и в пространстве.
Приведем без доказательства основные свойства расстояния в Rn:
1) 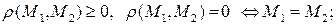
2)
3)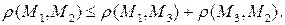
Замечание. Пространство Rn можно рассматривать и как векторное пространство. В этом случае упорядоченный набор чисел 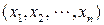 называется вектором пространства Rn. Векторы обычно обозначают строчными латинскими буквами:
называется вектором пространства Rn. Векторы обычно обозначают строчными латинскими буквами: 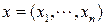 или
или 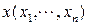 , или другими буквами. Нулевым вектором называют вектор
, или другими буквами. Нулевым вектором называют вектор 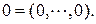
В векторном пространстве Rn вводятся операции сложения векторов и умножение векторов на число. Пусть 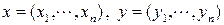 и
и 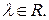 Тогда
Тогда
1)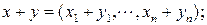
2)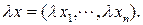
Векторное пространство Rn с операциями сложения и умножения на число называют также линейными или евклидовым пространством.
Определение. Длиной или нормой вектора 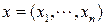 называется число
называется число

Для нормы вектора справедливы следующие свойства:
1)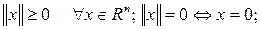
2)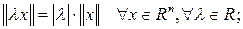
3)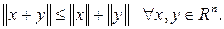
Определение. Скалярным произведением векторов 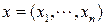 и
и 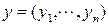 называют выражение
называют выражение
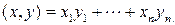
Не трудно доказать следующие свойства скалярного произведения:
 1)
1) 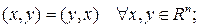
 2)
2) 
 3)
3) 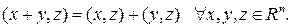
Определение. Пусть 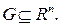 Функцией
Функцией 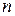 переменных называется отображенные
переменных называется отображенные  Значение функции
Значение функции 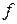
 записывается в виде
записывается в виде
 где
где 
При этом множество 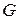 называется областью определения функции
называется областью определения функции 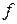 и обозначается
и обозначается 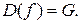
Замечание. Функцию n переменных можно записывать в привычном виде 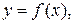 где
где 
 2014-02-02
2014-02-02 405
405






