2014-02-02
1860
2.1. Метод прямоугольников
Использует простейшую кусочно-ступенчатую аппроксимацию подинтегральной функции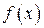 
на элементарных отрезках, заменяя ее постоянным значением 
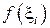. В качестве точек 
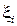можно принять левые 
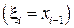, правые 
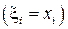границы или середину 
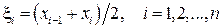элементарных отрезков. При этом интеграл заменяется интегральной суммой: 
.
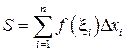При 
, например для метода прямоугольников, имеем:
.
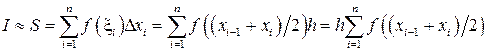2.2. Метод трапеций
Использует кусочно-линейную аппроксимацию функции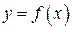 
по двум граничным точкам на каждом элементарном отрезке. Интеграл представляет собой сумму площадей элементарных трапеций:
,
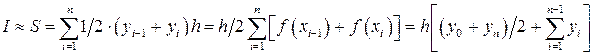где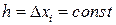 
.
2.3. Метод Симпсона
Отрезок интегрирования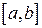 
разобьем на четное число 
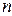равных частей с шагом 
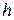. На каждом элементарном отрезке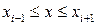 
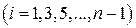подынтегральную функцию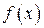аппроксимируем многочленом Лагранжа 2-й степени (через 3-и точки можно провести единственную параболу). Элементарная площадь 
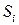может быть вычислена с помощью определенного интеграла: 
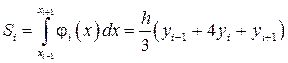, где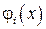 
– полином Лагранжа;
; 
; 
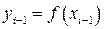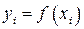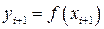. После суммирования 
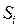имеем:
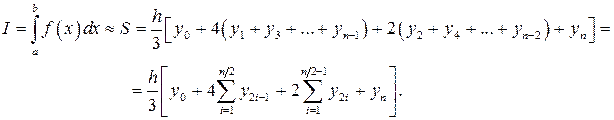
2.4. Погрешность численного интегрирования
|
|
|
Погрешность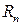
численного интегрирования равна:
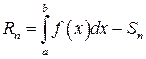и зависит от шага разбиения h интервала 
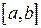. Её можно представить в виде 
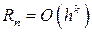─ порядка k (
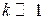). Из этого следует, что при 
, 
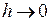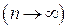значения интеграла, получаемые путем численного интегрирования, сходятся к его точному значению.
Главный член погрешности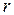 
формулы прямоугольников на каждом элементарном отрезке 
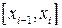равен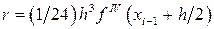 
, для формулы трапеций 
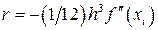. Главный член погрешности метода Симпсона имеет вид 
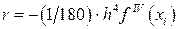, из чего следует, что метод Симпсона дает погрешность вычисления площади на каждом отрезке 
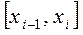~ в h /7,5 меньшую, чем метод прямоугольников.
При равноых интервале интегрирования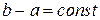 
и числе его разбиения n на элементарные отрезки метод прямоугольников имеет ошибку вычисления интеграла равную 
,
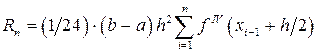а метод Симпсона (парабол) 
т.е. на порядок меньшую.
