Для вычисления производных функции 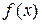 может быть использовано выражение:
может быть использовано выражение: 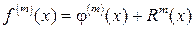 , где m – порядок производной;
, где m – порядок производной; 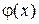 – функция, аппроксимирующая функцию
– функция, аппроксимирующая функцию 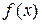 ;
; 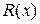 – погрешность аппроксимации функции
– погрешность аппроксимации функции 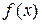 . В качестве
. В качестве 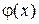 можно принять частичную сумму ряда или интерполяционную функцию. Тогда
можно принять частичную сумму ряда или интерполяционную функцию. Тогда  определяется остаточным членом ряда или интерполяционной формулы. За приближенное значение производной
определяется остаточным членом ряда или интерполяционной формулы. За приближенное значение производной 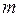 -го порядка
-го порядка 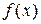 можно принять значение соответствующей производной
можно принять значение соответствующей производной 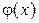 , то есть
, то есть 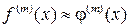 . Величина
. Величина 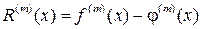 , характеризующая отклонение приближенного значения производной от ее истинного значения, называется погрешностью аппроксимации производной. При численном дифференцировании функции, заданной в виде таблицы с шагом
, характеризующая отклонение приближенного значения производной от ее истинного значения, называется погрешностью аппроксимации производной. При численном дифференцировании функции, заданной в виде таблицы с шагом 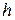 , эта погрешность зависит от
, эта погрешность зависит от 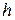 , и ее записывают в виде
, и ее записывают в виде 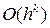 , где
, где 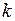 – показатель степени, называемый порядком погрешности аппроксимации производной. При этом принимается
– показатель степени, называемый порядком погрешности аппроксимации производной. При этом принимается 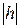 <1. Оценку погрешности можно проиллюстрировать с помощью ряда Тэйлора:
<1. Оценку погрешности можно проиллюстрировать с помощью ряда Тэйлора:
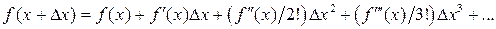 .
.
Если 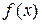 задана в виде таблицы значений
задана в виде таблицы значений 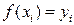 ,
, 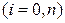 , то ряд Тэйлора с точностью до членов порядка
, то ряд Тэйлора с точностью до членов порядка 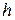 при
при 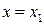 ,
, 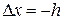 запишется:
запишется: 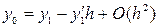 . Отсюда найдем значение производной в точке
. Отсюда найдем значение производной в точке 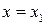 :
:
 .
.
 2014-02-02
2014-02-02 1319
1319
