Запишем полином 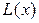 с равномерным расположением узлов
с равномерным расположением узлов 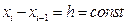 ,
, 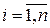 и его остаточный член
и его остаточный член 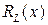 для случая 3-х узлов интерполяции (степень полинома n =2) и найдем их первые производные:
для случая 3-х узлов интерполяции (степень полинома n =2) и найдем их первые производные:
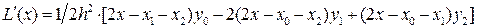 ;
;
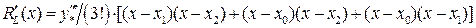 .
.
Для 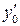 при
при 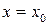 имеем:
имеем:
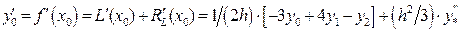 .
.
Аналогичные соотношения можно получить для 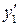 ,
,  при
при 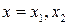 соответственно:
соответственно:
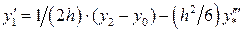 ,
, 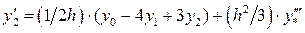 .
.
Таким образом, для 3-х узлов имеем 2-го порядка точность аппроксимации производных.
Для полинома Лагранжа и его остаточного члена в случае 4-х узлов (степень 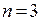 ) получим:
) получим:
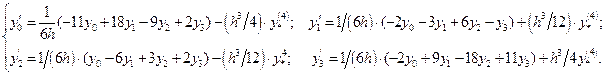
Таким образом, используя значения функции в 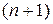 узлах, получаем аппроксимацию производных
узлах, получаем аппроксимацию производных 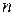 -го порядка точности. Можно показать, что при четных
-го порядка точности. Можно показать, что при четных 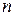 для производных в средних (центральных) узлах (
для производных в средних (центральных) узлах (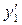 при
при 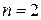 ,
, 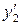 при
при 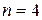 и т.д) получаются наиболее простые выражения и наименьшие коэффициенты в остаточных членах. Аппроксимации производных для узла с произвольным номером
и т.д) получаются наиболее простые выражения и наименьшие коэффициенты в остаточных членах. Аппроксимации производных для узла с произвольным номером 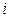 , считая его центральным, имеют вид:
, считая его центральным, имеют вид:
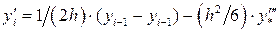 при
при 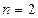 ;
;

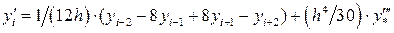 при
при 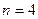 .
.
Они называются аппроксимациями производных с помощью центральных разностей и широко используются на практике!!!
С помощью интерполяционного полинома Лагранжа можно получить аппроксимации для старших производных. Например, аппроксимации вторых производных для 3-ёх узлов интерполяции имеют вид:
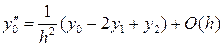 ;
;
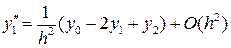 ;
;
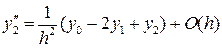 .
.
При этом аппроксимации вторых производных с помощью центральных разностей также наиболее выгодны.
 2014-02-02
2014-02-02 679
679







