2014-02-02
581
Для определения реакции ЛА на гармоническое воздействие в правую часть, например, (11.22) (k=1), подается сигнал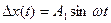 
. В этом случае на выходе вынужденная составляющая будет изменяться по гармоническому закону
,
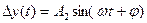где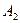 
и 
- амплитуда и частота вынужденных колебаний выходной величины,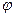 
- сдвиг по фазе. Величины 
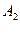и 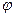весьма просто определяются по частотной функции 
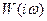, представляющей собой комплексную величину.
Можно показать, что 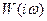получается из передаточной функции 
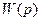путем замены
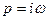, где - частота вынужденных колебаний.
Частотную функцию можно представить в виде
,
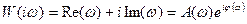где: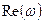 
, 
- соответственно вещественная и мнимая часть частотной функции;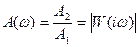 
- модуль частотной функции, называется амплитудно-частотнойхарактеристикой (АЧХ); 
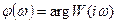- аргумент частотной функции, называется фазовой частотной характеристикой (ФЧХ). Для определения модуля и аргумента частотной функции 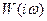изображается на комплексной плоскости для одного значения «» (см. рис. 65).
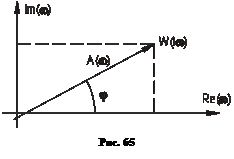Из этого рисунка видно, что
(при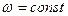 
)
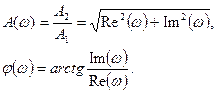
С помощью этих выражений можно строить амплитудную и фазовую частотные характеристики системы (звена) при изменении от 
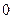до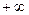 
.
|
|
|
Вопросы и задания для самостоятельной работы.
