Если рельс не может изменять длину при колебаниях своей температуры, то в нём возникают температурные силы Р t, прямо пропорциональные изменению температуры рельса относительно нейтральной температуры и не зависящие от длины рельса L.
Другими словами- величины температурных продольных сил в рельсе, который не может изменять свою длину, от длины рельса не зависят.
Пример 1.3 .Путь с рельсами Р65 длиной 25 м уложен с нулевыми зазорами в рельсовых стыках при температуре 19ºС. Рельс не может увеличивать свою длину. Какая продольная сила будет сжимать такой рельс при повышении его температуры до 49ºС?
Площадь поперечного сечения рельса Р65 равна F=82,7 см². Сжимающая рельс продольная температурная сила (см. формулу 1.4) будет равна
P t = σt F = α E F∆tр,
где F- площадь поперечного сечения рельса, см²;
α E=250 Н/см²∙град.
Р t =250∙82,7∙(49-19)=620250 Н.
Таким образом, в рельсе типа Р65 при невозможности изменения его длины
(нулевые стыковые зазоры) и повышении его температуры относительно нейтральной на 30º С возникает сжимающая продольная температурная сила более 62 т.
А если бы были уложены с нулевыми стыковыми зазорами рельса длиной 50 или 100 м? Продольная сжимающая температурная сила в рельсе в условиях примера не изменилась бы и составила также 620250 Н, или около 63248 кг, где 1кг=9,80665 Н.
Выше были рассмотрены предельные случаи – или рельс имеет полную свободу перемещений или не имеет возможности изменять свою длину вообще. А как изменяет свою длину рельс в зависимости от реальных условий?
В таких условиях это сопровождается преодолением сопротивлений, возникающих как за счёт действия сил трения при перемещении рельсов по подкладкам шпал или рельсов в балласте, а также концов рельсов в стыке.
В дальнейшем будем исходить из упрощенной схемы, когда силы сопротивления продольному смещению рельса, возникающие за счёт действия сил трения при перемещении рельсов по подкладкам шпал, или всей путевой решётки в балласте, равномерно распределены по всей длине рельса и не зависят от величины температурного изменения длины рельса. Эти силы сопротивления называют погонными и обозначают буквой q.
В рельсовом стыке накладки, стянутые болтами, создают силу сопротивления смещению конца рельса в стыке, которую считают одинаковой для всех стыков данного участка пути. Очевидно, что процесс изменения длины рельса не сможет начаться, пока возникающая при изменении температура рельса не сможет начаться, пока возникающая при изменении температуры рельса продольная температурная сила не превысит силу стыкового сопротивления. Величину изменения температуры рельса ∆tн, при которой это произойдёт, можно определить по следующей формуле
∆ t н = R / α E F, (1.5)
где R- величина стыкового скрепления, кг.
Пример 1.4. Рельсы Р65 длиной 25 м уложены при нейтральной температуре 18ºС со стыковыми зазорами 12 мм. Для таких рельсов при стандартной затяжке стыковых болтов можно принять величину сопротивления стыка R=100000 Н. Насколько должна измениться температура рельса, чтобы стыковое сопротивление было преодолено?
. Величину изменения температуры рельса ∆t н, при которой это произойдёт, можно определить по следующей формуле ∆t н = R /α E F,
где R- величина стыкового скрепления, кг
∆tн = 100000/(250∙82,7)≈5ºС.
Таким образом, при температуре рельса 23º С (18+5) стыковое сопротивление будет преодолено.
Если температура рельса повысится и превзойдёт 23ºС, то начинается перемещение концов рельса в пределах стыкового зазора и преодоление погонного сопротивления этому перемещению. При этом одновременно будет изменяться длина рельса и его напряжённое состояние. Поскольку в примере рассматривается рельс стандартной длины (25 м), то перемещения рельса такой относительно небольшой длины будут происходить в основном в пределах стыкового зазора.
На рис. 1.1 показано распределение продольных сил, возникающих в рельсах длиной L при изменении температуры рельса.
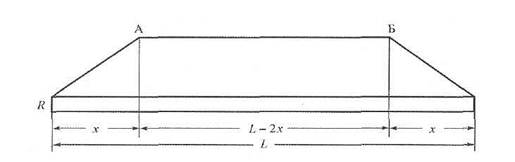
Рис. 1.1. Распределение продольных температурных напряжений по длине рельса: L- общая длина рельса; x- длина подвижной части рельса; (L-2x) – неподвижная часть рельса; R- стыковое сопротивление
При постоянном по длине рельса погонном сопротивлении p на длине рельса x возникает погонное сопротивление px, которое равномерно изменяется до нуля в конце рельса.
В сечениях А и Б возникнут напряжения σ t = p x / F. В промежутке между этими сечениями рельс не испытывает деформаций и работает как рельс, жёстко закрепленный по концам (см. формулу (1.3)). Длина активного концевого участка x может быть найдена из выражения
x = α EF∆t / p (1.6)
Анализ этой формулы показывает, что длина «активной» части рельса x прямо пропорциональна величине приращения температуры ∆t и обратно пропорциональна величине погонного сопротивления. Величина последнего зависит от типа, конструкции и состояния промежуточных скреплений, силы прижатия рельса к шпале, рода, состояния и степени уплотнения балластного слоя и ряда других причин. В предельном случае
x=0,5L.
Наибольшее изменение температуры, при котором полностью преодолеваются погонные сопротивления и продольные деформации распространяются по всей длине рельса, равно
Max t пог = 0,5 L p/α EF (1.7)
Рассмотрим общий случай изменения длины L рельса типа Р65, закреплённого на постоянный режим работы при температуре tо.
Величина удлинения конца рельса λ при преодолении погонного сопротивления определяется по формуле
λ = p x² / α E F. (1.8)
Длина подвижной части конца рельса при повышении его температуры на ∆t о составит
x = α EF∆t/p (1.9)
Смещение конца рельса при повышении его температуры на ∆ t равно
∆ L= 0,5 α x (∆t − ∆ tн). (1.10)
Пример 1.5. Рельсовая плеть длиной L=1200 м закреплена для работы в постоянном режиме при t з = 21º С в климатическом районе ст. Самара. Уравнительный пролёт состоит из трёх пар уравнительных рельсов длиной по 12,5 м. Величина каждого стыкового зазора δ Ф = 1,2 см.
Требуется:
- определить произойдёт ли смыкание зазоров при t max max.
- определить достигнет ли зазор конструктивного значения
(δ max = 2,1 см) при t min min.
Примем для решения остальные необходимые параметры (кроме известных в примерах 1-4):
t max max = 59º С, t min min= - 43 ºС,
стыковое сопротивление R=100000 Н, погонное сопротивление продольному смещению рельсовой плети р = 80 Н/см.
Смыкание зазоров в уравнительном пролете возможно только при повышении температуры. Диапазон температур (∆t+), при которых конец рельсовой плети смещается в сторону уравнительного пролета (с учетом сопротивления стыкового скрепления ∆ t н = 5 º С) для заданных t з = 21ºС и
t max max = 59ºС равен
∆t+ = tmax max – tз - ∆tн = 59 – 21 – 5 = 33 ºС
Определим длину х участка продольной деформации рельса при повышении его температуры до значения t max max = 59ºС относительно t з = 21ºС
Длина активного концевого участка x может быть найдена из выражения
x = α EF∆t + / p
x =250 Н/см.град·82,7 см² (59-21-5) / 80 Н/см = 8528 см
Смещение конца рельса при такой температуре после преодоления стыкового сопротивления равно
∆L+=0,5 α x ∆t+.
∆L+ =0,5·0,0000118·8528·33 = 1,7 см.
При повышении температуры для полного смыкания всех 4-х зазоров в уравнительном пролете конец рельсовой плети должен переместиться в сторону уравнительных рельсов на ∆L1+ = δ Ф * 4 = 12 *4 = 48 мм
Так как ∆L+ < ∆L1 +,то есть 17 мм < 48 мм, то смыкания зазоров в уравнительном пролете не произойдет.
Повторим расчеты для случая понижения температуры.
Раскрытие (увеличение) зазоров в уравнительном пролете возможно только при понижении температуры. Диапазон температур (∆t_-), при которых зазоры увеличиваются за счет смещения конца рельсовой плети в сторону её середины (с учетом сопротивления стыкового скрепления
∆t н = 5 º С) для заданных t з = 21ºС и t min min = - 43ºС равен
∆t_- = tз - ∆tн - t min min = 21 – 5 – (- 43) = 59 ºС
Определим длину х участка продольной деформации рельса при понижении его температуры до значения t min min = - 43ºС
x = α EF∆t- / p =250∙82,7∙59/80=15247см ≈152 м
Смещение конца рельса при понижении температуры после преодоления стыкового сопротивления равно
∆L=0,5 α x ∆ t -.
∆L - =0,5·0,0000118·15247·59 = 5,3 см.
При понижении температуры до t min min= - 43 º С для полного (конструктивного)раскрытия всех 4-х зазоров в уравнительном полете до
δ max = 2,1 см состояние зазоров позволят переместиться концу рельсовой плети в сторону середины плети на величину∆L1 -, значение которой определяется формулой
∆L1 - = (δ max - δ Ф) * 4 = (2,1 – 1,2)*4 = 3,6 см
Так как при интервале температур ∆t_- возможное перемещение конца плети ∆L - = 5,3 см, а для полного раскрытия зазоров достаточно ∆L1 - = 3,6 см, то есть ∆L- > ∆L1 - то в уравнительном пролете произойдет полное их раскрытие.
Пример 1.6 .Рельсовая плеть длиной L=1200 м закреплена для работы в постоянном режиме при t з = 21 º С в климатическом районе ст.Москва. Уравнительный пролёт состоит из трёх пар уравнительных рельсов длиной по 12,5 м. Величина каждого стыкового зазора δ Ф = 1,2 см.
Определим длину участка продольной деформации рельса при повышении температуры относительно нейтральной на 28 º С.
Примем стыковое сопротивление R=100000 Н, погонное сопротивление продольному смещению рельсовой плети р =80 Н/см.Тогда
x =250 Н /см град* 82,7*(28 -5)/ 80 Н/см = 5944 см.
Смещение конца рельса при такой температуре после преодоления стыкового сопротивления равно
λ = 0,5 * 0.0000118 1/град*5944 см *(28 -5)град = 0,81 см
На рис.1.1 показано распределение продольных сил в рельсе длиной L, концевые его участки длиной x=5944 см подвижны. Средняя часть рельса длиной (L-2x)=120000 см-2∙5944 см=108112 см при повышении его температуры относительно нейтральной на 28ºС осталась неподвижной.
Допустим, температура рельса достигла 53ºС, т.е. её повышение относительно температуры закрепления (нейтральной температуры tо=21ºС) составило ∆t=53-21=32ºС. В этом случае длина участка продольной деформации х и перемещение конца рельса ∆L будут следующими:
х=250∙82,7∙(32-5)/80=6978 см,
∆L=0,5∙0,0000118∙6978∙(32-5)=1,11 см.
Длина каждого подвижного конца рельса составит 6978 см, а средняя часть рельса длиной 120000-2∙6978=106044 см останется неподвижной. Эта часть останется неподвижной и при возможном дальнейшем повышении температуры (более 53ºС), поскольку стыковой зазор стал нулевым и дальнейшее удлинение рельса невозможно.
На неподвижной части рельса, сколь велика бы она ни была, величина продольных температурных сил, определяемых по формуле (1.4), будет зависеть только от разности температур рельса и закрепления t о.
Допустим, температура рельса достигла 58º С (такая температура является расчётной для Москвы). Продольная температурная сила в одном рельсе составит Р=250∙82,7∙(58-21)=764975 Н=78005 кг. По обоим рельсам продольная сжимающая сила составит около 156 т!
Допустим, что температура рельса зимой достигла величины – 42 º С (расчётная температура Москвы). Тогда при температуре закрепления плети +21º С продольная растягивающая рельс температурная сила
Рt=250∙82,7∙(-42-21)=-1302525 Н = -132820 кг.
Знак минус показывает, что в рельсе действует растягивающая сила.
При экстремальной зимней температуре рельса -42ºС растягивающая рельс сила превысила 132 т! Выдержит рельс такую растягивающую силу?
Изменяя температуру закрепления рельса на постоянный режим, можно регулировать величину продольной температурной сжимающей силы.
Если в условиях примера закрепить рельс не при +21ºС, а при +40ºС, то продольная сжимающая рельс сила летом при максимальной температуре составит всего
Рt=250∙82,7∙(58-40)=372150 Н=37949 кг.
По обоим рельсам продольная сжимающая сила составит около 76 т. Тогда зимой при самой низкой для Москвы температуре рельса -42ºС растягивающая его сила составит уже
Рt=250∙82,7∙(-42-40)=-1695350 Н=-172878 кг.
Отметим, что проведённые расчёты ещё раз показали важность правильного определения температуры закрепления рельсов на постоянный режим, а также важность правильного определения нейтральной температуры.
Физические пределы изменения температур рельсов в каждом регионе сети железных дорог ограничены. В «Технических указаниях по устройству, укладке, содержанию и ремонту бесстыкового пути» приведены расчётные температуры рельсов для сети железных дорог России.
В отдельных районах сети железных дорог расчётная летняя температура рельсов может достигать +65ºС, а расчетная зимняя температура -54ºС.
В условиях примера 1.6 при максимальной расчётной температуре рельса 65ºС и нейтральной температуре закрепления 21ºС сжимающая путевую решётку продольная температурная сила достигнет
Рt=2∙250∙82,7∙(65-21)=1819400 Н=185527 кг.
Таким образом, путевую решётку сжимает продольная температурная сила более 185 т.
1.3. Рельсы стандартной длины. Длинные рельсы. Бесстыковой путь.
Выше, в тексте рельсы назывались то рельсы нормальной (стандартной) длины, то длинные рельсы, то рельсовые плети, то длинные рельсовые плети. Какова же разница между этими понятиями?
Вернёмся к примеру 1.6. Рельсовая плеть была закреплена для работы в постоянном режиме при температуре закрепления (нейтральной температуре) tо=21ºС. После изменения температуры рельса на ∆tн=5ºС преодолеваются силы сопротивления, сдвигающие рельсы в стыке. Дальнейшее повышение температуры рельсов приводит к перемещению их концов в пределах стыкового зазора. После изменения температуры рельсов на величину ∆t = t н + max t пог полностью преодолеваются все силы сопротивления его продольной деформации. При дальнейшем изменении температуры в том же направлении рельс изменяет свою длину как свободный стержень (см. формулу (1.2)).
Пределы изменения температуры рельсов по станциям сети железных дорог указаны в «Технических указаниях по устройству, укладке, содержанию и ремонту бесстыкового пути». Наибольший перепад ∆ tmax может быть определён как разность между максимальной для данной местности температуры рельса tmax и температуры закрепления рельса на постоянный режим работы.
Если ∆tmax ≥ ∆t, то левый и правый (см. рис. 1.1) участки х смыкаются друг с другом, что является отличительным признаком отличия как рельсов обычной (нормальной) длины, так и длинных. Соотношения между величинами стыкового зазора δ и температурного перемещения конца рельса λ является дополнительным признаком отличия рельсов обычной длины от длинных рельсов.
Если температурное перемещение λ полностью компенсируется за счёт стыкового зазора δ, то перед нами рельс обычной длины.
При расчётных значениях стыкового зазора 19 и 21 мм, начиная с температурной амплитуды 85ºС и выше, рельс длиной 25 м почти никогда нельзя отнести к категории «рельс обычной длины». Другими словами, одна и та же конструкция пути с рельсами длиной 25 м в зависимости от температурной зоны может быть отнесена как к рельсам обычной длины, так и к длинным рельсам.
Если длина рельса такова, что для компенсации перемещения его концов недостаточно стыкового зазора δ и в процессе удлинения рельса полное закрытие стыкового зазора наступает прежде, чем температура рельса достигает максимума (тогда дальнейшее повышение температуры приводит к торцевому нажатию концов рельсов в стыке), а полное конструктивное раскрытие стыкового зазора наступает прежде, чем температура рельса достигнет минимума (тогда при дальнейшем понижении температуры стыковые болты начинают работать на изгиб),- в этом случае перед нами длинный рельс.
В зависимости от расчётной для данной местности амплитуды экстремальных температур рельсов, типа, конструкции и состояния промежуточных и стыковых скреплений, рода и состояния балластного слоя, величины установленных при укладке стыковых зазоров и некоторых других причин длина длинного рельса на сети дорог может изменяться от 25 до 150 м.
Если ∆t > ∆t max то температурные деформации возникают лишь на концевых участках рельса. Средняя его часть при любых изменениях температуры всегда будет неподвижной, это является необходимым и достаточным признаком бесстыкового пути.
Бесстыковой путь-условное название железнодорожного пути, рельсы которого на ряду с «активными» концевыми участками при любых изменениях реальных температур рельсов имеют не подвижную среднюю часть.
В официальном документе («ТУ-2000») дано иное определение: «Бесстыковой путь- железнодорожный путь, имеющий рельсы столь большей длины, что в них при изменениях температуры возникают продольные силы, пропорциональные этим значениям», т.е. за классификационный признак принято наличие температурных продольных сил.
Нам представляется, что более точным классификационным признаком бесстыкового пути является наличие в рельсовых плетях бесстыкового пути неподвижной средней части рельса при максимально возможных в данной местности изменения температур рельсов.
Отличительные признаки рельсов различной длины
Таблица 1.1
| Термин | Зона распространения температурных деформации | Изменение стыкового зазора |
| Рельс обычной длины | По всей длине рельса | λ >max λ > 0 |
| Длинный рельс | То же | λ = 0 при t < tmax max λ=λmax при t >tmin min |
| Бесстыковой путь | Только на концевых участках | _ |
Из таблицы видно, что из-за отсутствия стыков внешне более простой, чем звеньевой, бесстыковой путь на большей части рельсовой плети нагружен значительными по величине продольными температурными силами.
2.1. Как обеспечить прочность рельсовых плетей бесстыкового пути?
Очевидно, что бесстыковой путь должен быть прочен и устойчив. В зимний период при температурах рельса ниже температуры закрепления плетей на постоянный режим, когда рельсовые плети растянуты продольными температурными силами, необходимо обеспечить прочность рельсовых плетей на разрыв.
В основу расчёта прочности рельсовых плетей бесстыкового пути положено условие, чтобы суммарное основное напряжение, возникающее в рельсе от воздействия подвижного состава и в результате изменения температуры, не превосходило допустимого напряжения.
Главное условие достаточности запасов прочности рельсовых плетей в конкретных эксплуатационных условиях имеет вид:
 (2.1)
(2.1)
где 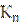 - коэффициент запаса прочности рельсов на растяжение.(Для рельсов первого срока службы и старогодных рельсовых плетей, прошедших диагностирование и ремонт в стационарных условиях или профильное шлифование и диагностирование в пути,
- коэффициент запаса прочности рельсов на растяжение.(Для рельсов первого срока службы и старогодных рельсовых плетей, прошедших диагностирование и ремонт в стационарных условиях или профильное шлифование и диагностирование в пути,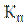 =1,3; для рельсов, пропустивших нормативный тоннаж или переложенных без шлифования,
=1,3; для рельсов, пропустивших нормативный тоннаж или переложенных без шлифования,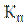 =1,4; для рельсов укладываемых на второстепенных путях,
=1,4; для рельсов укладываемых на второстепенных путях, 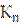 =1,2;
=1,2;
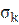
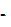 напряжение в кромках подошвы рельсовых плетей при проходе подвижного состава);
напряжение в кромках подошвы рельсовых плетей при проходе подвижного состава);
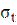 – напряжение в поперечном сечении рельса от действия продольных растягивающих сил(температурных, сил угона);
– напряжение в поперечном сечении рельса от действия продольных растягивающих сил(температурных, сил угона);
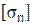 - допустимое напряжение(для сырых рельсов
- допустимое напряжение(для сырых рельсов 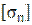 =350МПа; для новых термоупрочнённых рельсов
=350МПа; для новых термоупрочнённых рельсов 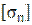 =400МПа).
=400МПа).
Кромочные напряжения в рельсовых плетях 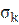 определяются по специальной методике («Правила расчёта верхнего строения пути на прочность») с учётом типа, серии, осевых нагрузок, скоростей движения обращающего по данному участку подвижного состава; с учётом типа, рода и состояния элементов верхнего строения бесстыкового пути.
определяются по специальной методике («Правила расчёта верхнего строения пути на прочность») с учётом типа, серии, осевых нагрузок, скоростей движения обращающего по данному участку подвижного состава; с учётом типа, рода и состояния элементов верхнего строения бесстыкового пути.
В основу расчёта прочности рельсовых плетей бесстыкового пути положена теория изгиба рельса как балки на сплошном упругом основании. В качестве действующей на путь силы рассматривается нагрузка, идущая от колеса и являющаяся суммой статической нагрузки и динамической добавки, которая зависит от скорости движения, особенностей самого экипажа и увеличивается с ростом скорости движения.
Модуль упругости подрельсового основания зимой в этих расчётах при железобетонных шпалах с резиновыми нашпальными и подрельсовыми упругими прокладками может быть принят равным 120 и 130 МПа при эпюрах шпал соответственно 1840 и 2000 шт./км. Модуль упругости подрельсового основания численно равен силе, приложенной к пути длинной 1 см и вызывающей его упругую просадку на 1 см.
При совместном действии внецентренно приложенных вертикальных и поперечных сил от поездной нагрузки в кромке подошвы (наиболее напряжённом месте рельса зимой) возникают напряжения изгиба и кручения до 100 - 200 МПа.
Температурные напряжения, возникающие в рельсе в связи с несостоявшимся при изменении температуры изменением его длины, определяются по формуле (1.3).
С учётом формул (1.3) и (2.1) можно записать формулу для определения наибольшего допустимого понижения температуры рельсовой плети по сравнению с температурой при закреплении:

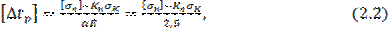
 В Приложении 2 «Технических указаний по устройству, укладке, содержанию и ремонту бесстыкового пути» приведены допустимые понижения температуры рельсов для бесстыкового пути с термоупрочнёнными рельсами типа Р65 первого срока службы на железобетонных шпалах и щебёночном или асбестовом балласте в зависимости от типа обращающегося локомотивов, скоростей движения и радиусов кривых.
В Приложении 2 «Технических указаний по устройству, укладке, содержанию и ремонту бесстыкового пути» приведены допустимые понижения температуры рельсов для бесстыкового пути с термоупрочнёнными рельсами типа Р65 первого срока службы на железобетонных шпалах и щебёночном или асбестовом балласте в зависимости от типа обращающегося локомотивов, скоростей движения и радиусов кривых.
В качестве примера приведём допускаемые по условию прочности рельсов значения 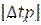 для локомотива ВЛ80:
для локомотива ВЛ80:
| Скорость, км/ч | Допустимое понижение температуры 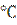 | ||||||||
| В прямом участке, м | В кривой радиусом, м | ||||||||
| - | - | ||||||||
| - | - | - |
Пример 2.1. В условиях Московской железной дороги определить допустимое по отношению к температуре закрепления рельсовой плети понижение температуры 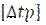 для бесстыкового пути из новых термоупрочнённых рельсов типа Р65 с железобетонными шпалами, скреплением КБ65 и щебёночным балластом из скальных пород на блок - участке протяжением 2500 м, где имеются две кривые радиусом 1400 м (эпюра шпал 1840 шт./км) и 500 м (эпюра шпал 2000 шт./км). На участке обращается электровоз ВЛ80 со скоростью 100 км/ч.
для бесстыкового пути из новых термоупрочнённых рельсов типа Р65 с железобетонными шпалами, скреплением КБ65 и щебёночным балластом из скальных пород на блок - участке протяжением 2500 м, где имеются две кривые радиусом 1400 м (эпюра шпал 1840 шт./км) и 500 м (эпюра шпал 2000 шт./км). На участке обращается электровоз ВЛ80 со скоростью 100 км/ч.
В соответствии с приведёнными в таблице данными: для прямого участка 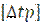 =96
=96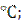 для кривой радиусом 1400 м
для кривой радиусом 1400 м 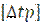 =90
=90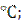 для кривой радиусом 500 м
для кривой радиусом 500 м 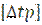 =82
=82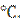
2.2 Устойчивость бесстыкового пути и определяющие её факторы.
Обеспечение устойчивости - одна из основных проблем устройства и содержания бесстыкового пути. Обычно рассматривают несколько причин, влияющих на возникновение предельного состояния бесстыкового пути по устойчивости при движении поездов.
Первая причина заключается в том, что перед движущимся колесом возникает зона, где рельс несколько приподнимается по сравнению со своим исходным положением. В этой зоне отрицательного прогиба максимальный подъём рельса составляет всего 4% от прогиба под колесом. Однако и при таком небольшом его поднятии уменьшаются силы сцепления шпал со щебёночным основанием и сопротивление пути перемещению.
Вторая причина - изменяется устойчивость пути при его вибрации позади и впереди движущегося поезда.
Третья причина - происходит угон пути. При наличии надёжной упругой связи рельсовых плетей с основанием эти силы относительно не велики. Однако, если на длине плети имеются участки, где плохо закреплены клеммы промежуточных скреплений, при проходе поезда по ним возникают местные подвижные плети с образованием на их концах значительных по величине дополнительных сил сжатия или растяжения. Складываясь с температурными продольными силами, они могут вызвать нарушение устойчивости путевой решётки.
Критическую продольную сжимающую силу, которая вызывает потерю устойчивости путевой решётки, стремились определить как теоретически, так и экспериментально.
Известны различные теоретические подходы к определению критической силы, разработанные в России К.Н. Мищенко, С.П. Першиным, С.И. Морозовым, А.Я. Коганом и другими учёными. В последние годы М.Ф. Вериго предложен метод имитационного моделирования устойчивости бесстыкового пути. А.Я. Коганом разработана методика расчёта устойчивости бесстыкового пути, учитывающая взаимосвязь критической сжимающей силы в рельсовых плетях с размерами неровностей в прямых и кривых участках пути.
Экспериментальные исследования включают в себя как определение отдельных характеристик сопротивляемости бесстыкового пути и отдельных его элементов выбросу (силы сопротивления шпал перемещениям и промежуточных скреплений повороту рельса, моменты инерции путевых решёток и др.), так и создание специальных участков пути - стендов, на которых воссоздаются условия и изучаются процессы, сопровождающие процесс потери устойчивости бесстыкового пути.
Важнейшее значение имели результаты экспериментальных исследований, проведённых в 60-х гг. прошлого века под руководством Е.М. Бромберга на опытном стенде ВНИИЖТа. Наблюдения за искривлением путевой решётки на стенде при нагревании рельсов позволили выяснить, как протекает процесс потери устойчивости. Было установлено, что при существующих соотношениях жёсткости пути в горизонтальной и вертикальной плоскостях процесс потери устойчивости проходит лишь в горизонтальной плоскости.
До некоторого значения температуры 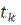 продольная сжимающая сила возрастает до величины
продольная сжимающая сила возрастает до величины 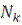 , причём поперечные перемещения путевой решётки при этом не происходят. При дальнейшем повышении температуры появляются нелинейно изменяющиеся такие перемещения путевой решётки, растущие сначала медленно, а затем при достижении некоторой температуры
, причём поперечные перемещения путевой решётки при этом не происходят. При дальнейшем повышении температуры появляются нелинейно изменяющиеся такие перемещения путевой решётки, растущие сначала медленно, а затем при достижении некоторой температуры 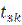 - весьма быстро. На конечной стадии перемещения приобретают динамический характер и происходит выброс пути.
- весьма быстро. На конечной стадии перемещения приобретают динамический характер и происходит выброс пути.
Если нагревание рельсовых плетей прекращалось в интервале температур рельсов от 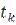 до
до 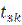 и в дальнейшем они остывали, то путь оставался деформированным. При повторном нагревании уже искривлённого пути выброс происходил, когда значения температур были они уже меньше.
и в дальнейшем они остывали, то путь оставался деформированным. При повторном нагревании уже искривлённого пути выброс происходил, когда значения температур были они уже меньше.
Е.М. Бромберг предложил конструкцию и интервалы закрепления рельсовых плетей бесстыкового пути выбирать следующим образом, чтобы предотвратить наступление первого критического состояния- начала подвижек путевой решётки.
Наблюдения показали, что при потере устойчивости бесстыкового пути в кривых участках выброс происходит всегда наружу кривой. Сначала возникает поперечная сдвижка путевой решётки на небольших по длине участках(8-12м). Непосредственно перед выбросом наружняя рельсовая плеть в кривых при щебёночном балласте в плане имеет отклонения от первоначального положения, равные 15-25 мм, а при асбестовом балласте всего 5- 6 мм.
Допустимое по условиям обеспечения устойчивости бесстыкового пути повышение температур рельсов было определено в ходе экспериментальных исследований, на основании которых в Приложении 2 к «Техническим указаниям по устройству, укладке, содержанию и ремонту бесстыкового пути» даны значения величин для вновь уложенных или переложенных повторно рельсовых плетей при различных конструкциях верхнего строения пути.
для вновь уложенных или переложенных повторно рельсовых плетей при различных конструкциях верхнего строения пути.
В качестве примера приведём значения допустимого повышения температур рельсовых плетей бесстыкового пути с балластным слоем из щебня скальных пород.
| Тип рельсов | Эпюра шпал, шт./км | Допустимое повышение температур рельсов  | |||||||
| в прямом участке, м | в кривых радиусом, м | ||||||||
| Р65 | |||||||||
| - |
Пример 2.1. (продолжение).
Определим допустимое по условию обеспечения устойчивости бесстыкового пути повышение температур. Оно составит при эпюре шпал 1840 шт./км для прямого участка - 54 ; для кривой радиусом 1400 м - 48
; для кривой радиусом 1400 м - 48 (получено интерполяцией); для кривой радиусом 500 м - 39
(получено интерполяцией); для кривой радиусом 500 м - 39 ; при эпюре шпал 2000 шт./км для прямого участка - 58
; при эпюре шпал 2000 шт./км для прямого участка - 58 ; для кривой радиусом 1400 м - 52
; для кривой радиусом 1400 м - 52 (получено интерполяцией); для кривой радиусом 500 м- 41
(получено интерполяцией); для кривой радиусом 500 м- 41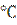 .
.
2.3 Диаграмма температурной работы бесстыкового пути и определение допустимого интервала закрепления рельсовых плетей на постоянный режим.
При каких же эксплуатационных условиях возможна укладка бесстыкового пути?
Возможность укладки бесстыкового пути в конкретных условиях устанавливается сравнением допускаемой температурной амплитуды 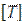 с фактически наблюдавшейся в данной местности амплитудой колебания температуры
с фактически наблюдавшейся в данной местности амплитудой колебания температуры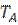 .
.
Значение 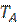 определяется как алгебраическая разность наивысшей
определяется как алгебраическая разность наивысшей 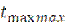 и наинизшей
и наинизшей 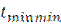 температур рельсов, наблюдавшихся в данной местности.
температур рельсов, наблюдавшихся в данной местности.
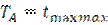 -
- 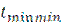 . (2.3)
. (2.3)
Амплитуда допустимых по условиям прочности и устойчивости бесстыкового пути изменений температур рельсов равна:
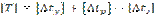 , (2.4)
, (2.4)
где 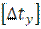 - допустимое по условию обеспечения устойчивости при повышении температуры рельсовых плетей по сравнению с температурой их закрепления;
- допустимое по условию обеспечения устойчивости при повышении температуры рельсовых плетей по сравнению с температурой их закрепления;
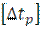 - допустимое по условию обеспечения прочности рельсовых плетей понижение температуры рельсов по сравнению с температурой их закрепления;
- допустимое по условию обеспечения прочности рельсовых плетей понижение температуры рельсов по сравнению с температурой их закрепления;
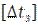 - минимальный интервал температур, в котором должны быть закреплены рельсовые плети на постоянный режим.
- минимальный интервал температур, в котором должны быть закреплены рельсовые плети на постоянный режим.
Интервал 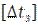 обычно принимается равным 10
обычно принимается равным 10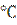 . В случае применения средств принудительного ввода рельсовых плетей в расчётный интервал (растягивающие и нагревательные установки) интервал
. В случае применения средств принудительного ввода рельсовых плетей в расчётный интервал (растягивающие и нагревательные установки) интервал 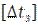 может быть принят равным 5
может быть принят равным 5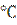 .
.
Если 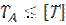 , то в заданных климатических и эксплуатационных условиях возможна укладка бесстыкового пути без сезонных разрядок напряжений.
, то в заданных климатических и эксплуатационных условиях возможна укладка бесстыкового пути без сезонных разрядок напряжений.
Пример 2.1.(продолжение ). Определим возможность укладки бесстыкового пути без сезонных разрядок напряжений. Ранее определили, что при скорости движения электровоза ВЛ80 100 км/ч по блок - участку длиной 2500 м с кривыми участками пути радиусами 1400 и 1500 м:
Для прямой 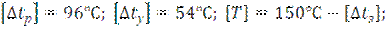
Для кривой 1400 м 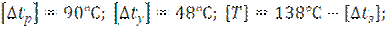
Для кривой 500 м 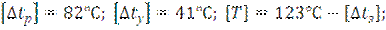
В условиях Московской железной дороги(район станции Рязань)
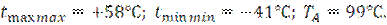
Сопоставляя 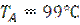 со значениями
со значениями 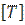 при
при 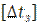 = 10
= 10 для блок- участка длинной 2500 м, делаем вывод, что для всех элементов плана в условиях примера укладка бесстыкового пути без сезонных разрядок напряжений возможна.
для блок- участка длинной 2500 м, делаем вывод, что для всех элементов плана в условиях примера укладка бесстыкового пути без сезонных разрядок напряжений возможна.
Расчётный интервал закрепления рельсовых плетей
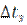 =
=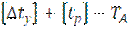 (2.5)
(2.5)
Границы расчётного интервала закрепления, т. е. самую низкую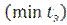 и самую высокую
и самую высокую 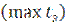 температуры закрепления определяют по формулам:
температуры закрепления определяют по формулам:
 =
= 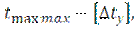 (2.6)
(2.6)
 =
= 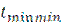
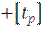 . (2.7)
. (2.7)
В условиях примера границы интервала закрепления рельсовых плетей на постоянный режим будут равны:
Для прямых участков 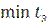 =58
=58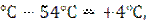
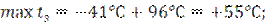
Для кривой 1400 м 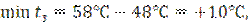
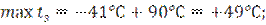
Для кривой 500 м 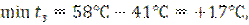
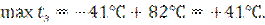
Рельсовая плеть на всём своём протяжении должна быть закреплена на постоянный режим работы в одном интервале температур, границы которого определяются наиболее высокой из рассчитанных 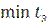 и наиболее низкой из рассчитанных
и наиболее низкой из рассчитанных 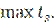
В условиях примера 2.1. для всей плети длиной 2500 м принимается
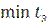 = + 17º C,
= + 17º C, 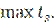 = + 41º С
= + 41º С
В «Технических указаниях по устройству, укладке, содержанию и ремонту бесстыкового пути» приводится так же таблица оптимальных температур закрепления плетей на железных дорогах России (табл.2.1.)
Таблица2.1
| Железная дорога | ||
| Общая | ||
| Октябрьская | 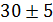 | |
| Калининградская | 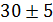 | |
| Московская | 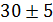 | |
| Горьковская | 25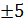 | |
| Северная | 25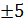 | |
| Северо- Кавказская | 35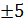 | |
| Юго-Восточная | 35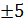 | |
| Приволжская | 35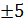 | |
| Куйбышевская | 30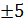 | |
| Свердловская | 25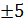 | |
| Южно-Уральская | 30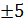 | |
| Западно- Сибирская | 30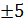 | |
| Красноярская | 25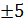 | |
| Восточно-Сибирская | 25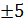 | |
| Забайкальская | 25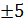 | |
| Дальневосточная | 30 |
Образец температурной диаграммы приведен на рис.2.1.
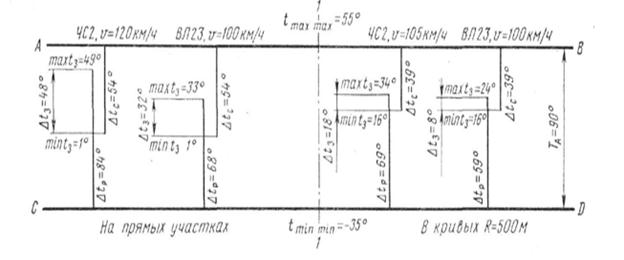
Рис.2.1. Температурная диаграмма работы бесстыкового пути с рельсами Р65 на щебне
 2014-02-02
2014-02-02 9592
9592








