Сети Петри. Маркировка

Множество входных и выходных позиций перехода t_i Î T обозначим через I(t_i) и O(t_i) соответственно. Аналогично, записи I(p_i) и O(p_i) есть обозначения входного и выходного множеств переходов для позиции pi. Тогда сеть Петри может быть задана как формальная система следующим образом:

S = < P, T, I, O, m⁰ >, где I = 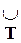I (ti), O = 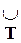O (ti), P = I È O.

Представление сети Петри в виде двудольного графа позволяет задать структуру сети Петри статически. Динамика в модель вносится механизмом смены маркировки (разметки) позиций и соглашением о правиле срабатывания (реализации) переходов.

Начальная маркировка присваивает позициям сети Петри целые числа (в том числе нуль).

На графе маркировка задается следующим образом: в позициях проставляют определенное число точек, носящих название маркеров или фишек. Передвижение маркеров по сети осуществляется посредством срабатывания ее переходов. Сработать может только возбужденный переход, то есть такой переход t_i Î T, во всех входных позициях которого содержится хотя бы по одному маркеру. Срабатывание перехода может произойти через любой конечный промежуток времени после возбуждения перехода. Результатом срабатывания является изъятие по одному маркеру из каждой входной позиции срабатывающего перехода и добавление маркера во все его выходные позиции. Изъятие маркеров и их перемещение считается мгновенным, с нулевой задержкой. Срабатывание какого-либо возбужденного перехода вызывает смену маркировки сети. Текущая маркировка сети понимается как состояние сети в данный момент времени. Можно считать, что динамика поведения сети Петри (ее функционирование во времени) адекватно может быть описана моделью вида: S = < m⁰, ®, m >, где m⁰ - начальная маркировка; ® - отношение следования маркировок; m - множество допустимых маркировок данной сети достижимых из m⁰.

Маркировка может задаваться вектором m = (m₁,... m_n ), число компонент которого соответствует числу позиций сети. Значение i - й компоненты i £ n есть натуральное число равное числу маркеров в позиции.

Пример. Для сети Петри, заданной в виде графа:

P1 P2

t1

P3 P4

t2 t3 t4

t5

P5 P6 P7

рассмотреть следование маркировок из m⁰.

Решение. Начальная маркировка имеет следующий вид:

m⁰ = (2, 1, 0, 0, 0, 1, 0), где цифра есть число маркеров в соответствующей позиции. По определению возбужденным переходом сети при маркировке m⁰ является переход t1. Его срабатывание приводит сеть в новое состояние

m⁰ ® m¹, m¹ =(1, 0, 1, 1, 0, 1, 0). Далее возбуждаются переходы t4, t2, t3. Из переходов t2 и t3 может сработать только один, так как срабатывание одного перехода снимает возбуждение другого. Рассмотрим все возможные варианты:

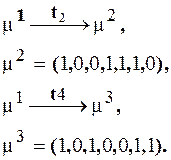
Отметим, что в сети возможно одновременное срабатывание нескольких переходов, например, (t2, t4) или (t3, t4) после срабатывания перехода t1. Рассмотрим соответствующие этим вариантам состояния сети:

m⁰ ® m¹ ® m⁴, m⁴ = (1, 0, 0, 0, 1, 1, 1) - при срабатывании (t2, t4),

m⁰ ® m¹ ® m⁴, m⁴ = (1, 0, 0, 0, 1, 1, 1) - при срабатывании (t3, t4).

Для задания динамики сети Петри используют диаграмму достижимых состояний (маркировок). Диаграмма представляет собой ориентированный граф, вершины которого есть достижимые маркировки из множества M, а дуги направлены из m^a в m^b . Дуги, если необходимо, помечают обозначением тех переходов, срабатывание которых является причиной смены маркировки.

Пример. Построить диаграмму достижимых состояний для сети предыдущего примера.

Решение.

(2, 1, 0, 0, 0, 1, 0)

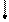t1

(1, 0, 1, 1, 0, 1, 0)

t2Èt3 (t2Èt3)&t4 t4

(1, 0, 0, 1, 1, 1, 0) t2Èt3 (1, 0, 1, 0, 0, 1, 1)

t4

(1, 0, 0, 0, 1, 1, 1) t5

t5 t2Èt3 (1, 1, 1, 0, 0, 1, 0)

(1, 1, 0, 0, 1, 1, 0)

t1 t2Èt3 t1

(0, 0, 1, 1, 1, 1, 0) (0, 0, 2, 1, 0, 1,0)

t2Èt3 t4 (t2Èt3)&t4 t4

(t2Èt3)&t4 t2Èt3 (0, 0, 2, 0, 0, 1,1)

(0, 0, 0, 1, 2, 1, 0) (0, 0, 1, 0, 1, 1, 1) t5

t4 t5 (0, 1, 2, 0, 0, 1,0)

(0, 0, 0, 0, 2, 1, 1) t2Èt3 t2Èt3

t5 t2Èt3 (0, 1, 1, 0, 1, 1,0)

(0, 1, 0, 0, 2, 1, 0)

(t2Èt3)&t4 - означает, что одновременно может сработать одна из пар

переходов: (t2Èt4) или (t3Èt4). Диаграмма отражает возможность параллельности вычислительных процессов. В рассматриваемом примере множество допустимых маркировок (состояний) равно 16. Причем из выделенной в качестве начальной маркировки m⁰ достижима лишь одна заключительная (тупиковая) маркировка m^T = (0, 1, 0, 0, 2, 1, 0), из которой уже не может идти продвижение маркеров по сети. Это гарантирует однозначное завершение процесса, моделируемого сетью. По диаграмме можно проследить множество последовательностей срабатывания переходов (траекторий процесса). Одна из возможных траекторий: t1 t3 t4 t5 t1 t4 t5 t2.

В общем случае, начальной маркировке может соответствовать несколько результирующих маркировок. Достижение каждой из них возможно при определенном распределении скоростей срабатывания переходов. В общем случае в некоторых позициях сети Петри возможно накопление бесконечного числа маркеров. Следовательно, множество допустимых состояний может не быть конечным. В сети Петри может не существовать тупиковых маркировок. Такого рода сетями моделируются циклические или автономные процессы.