Кодирование автомата

Модели автоматов Мили и Мура

В классе синхронных конечных автоматов рассматриваются два типа автоматов: модель Мура и модель Мили [5]. Модель Мили (автомат Мили) описывается функцией переходов вида: q (t + 1) = j (a (t), q (t)) и функцией выходов вида: l (t) = x (a (t), q (t)), где a (t) - состояние входа, q (t) - внутреннее состояние автомата. Состоянием автомата считаем пару

(a (t), q (t)).

Модель Мура (автомат Мура) определяется функцией переходов вида:

q (t + 1) = j (a (t), q(t)) и функцией выходов вида: l (t) = y (q (t)).

Выход автомата Мура определяется только внутренним состоянием автомата и не зависит от состояния входа в момент времени t. Такой автомат может рассматриваться как частный случай автомата Мили. Действительно, для автомата Мура можно записать q (t) = j (a (t - 1), q (t - 1)), следовательно, l(t) = (a(t - 1), q(t - 1)).

Различие между автоматами Мили и Мура состоит в том, что в автомате Мили состояние выхода возникает одновременно с вызывающим его состоянием входа, а в автомате Мура - с задержкой на один такт.

Поведение синхронного автомата определяется уравнениями:

n модель Мили:

q (t + 1) = j (a (t), q (t)); l (t + 1) = x (a (t + 1), q (t+1))

n модель Мура:

q (t + 1) = j (a (t), q (t)); l(t + 1) = (a(t), q(t)).

Поведение асинхронного автомата определяется уравнениями:

q (t + 1) = j (a (t + 1), q (t));

l (t + 1) = x (a (t + 1), q (t + 1)).

Как правило, во многих случаях состояния входа и выхода автомата являются закодированными и задача кодирования автомата сводится к кодированию (размещению) его внутренних состояний [5]. Каждый реальный элемент памяти вносит определенную задержку, которая зависит от свойств данного элемента памяти. Элементы памяти даже одного типа могут иметь различные задержки сигналов. Если на вход двух элементов памяти подать одновременно сигнал, то сигналы на выходах могут появиться не одновременно. С этим обстоятельством связано явление, которое называется состязанием элементов памяти.

Каждому внутреннему состоянию автомата в результате кодирования сопоставляется определенная кодовая комбинация, состоящая из нулей и единиц. Кодовая комбинация характеризует состояние элементов памяти.

Пример. Как показано ниже на рисунке, автомат из внутреннего состояния x_i под действием состояния входа a_r может попасть в состояние x_j, а также может попасть в состояния x_k и x_l в зависимости от того, какой элемент памяти раньше изменит свое состояние, если возможность таких переходов отражена в таблице переходов автомата

x_k 0 1 0

a_r a_r

a_r x_j

x_i 1 0 0

0 0 0 a_r a_r

x_l a_r

0 0 1 x_m

1 0 1

Если затем при том же состоянии входа a_r автомат из x_k или x_l перейдет во внутренне состояние x_j, то такие состязания элементов памяти называются допустимыми (не критическими). Для того, чтобы при этом не искажалась и функция выходов автомата, с состояниями (ar, xk) и (ar, xl) нужно сопоставить то же состояние выхода, что и с состоянием (ar, xj). Если же автомат из x_l или x_k при состоянии входа a_r перейдет в какое-либо другое внутреннее состояние или не изменит своего внутреннего состояния, то такие состязания являются критическими, то есть недопустимыми. Речь идет о недетерминированном конечном автомате.

Будем говорить, что автомат работает устойчиво, если в процессе его работы не возникают критические состязания элементов памяти, в противном случае - автомат будет работать не устойчиво, что не допустимо.

Кодирование состояний автомата можно выполнить двумя способами. Первый способ предусматривает, чтобы всем соседним внутренним состояниям, то есть таким, между которыми должны быть переходы, приписывались соседние кодовые комбинации. Такой способ требует повышенного числа элементов памяти. Второй способ касается кодирования, допускающего некритические состязания элементов памяти. При таком кодировании сокращается число элементов памяти по сравнению с первым вариантом кодирования. Оба способа имеют свои преимущества и недостатки.

Рассмотрим первый вариант кодирования, при котором всем внутренним состояниям, между которыми в таблице переходов есть переходы приписываются соседние кодовые комбинации, отличающиеся одной цифрой.

Пример. Закодировать состояния автомата, представленного следующей таблицей переходов (в таблице принято сокращение записи, т.е. q_i представлено просто числом i):

	a1	a2	a3	код
q1
q2
q3
q4
q5
q6
q7
q8

Решение. Из первой строки видно, что между состоянием q1 и q2 или q4 существуют переходы, значит, этим состояниям можно приписать следующие кодовые комбинации: q1 ® 000, q2 ® 001, q4 ® 010. Аналогично кодируются оставшиеся состояния. Ниже приведен граф, описывающий последовательность кодирования состояний автомата.

2 3 8 6

1 4 7 5

Такой способ кодирования может потребовать повышенного числа элементов памяти из - за наличия большого числа переходов для возможно одного состояния. В ряде случаев, допустив некритические состязания, можно осуществить кодирование при меньшем числе элементов памяти.

Если в графе переходов имеется контур нечетной длины, то закодировать такой автомат соседним кодом без введения дополнительных внутренних состояний не возможно (направление следования при этом не имеет значения).

Пример. Для автомата, представленного таблицей переходов

	a1	a2	a3	Код
q1
q2
q3
q4
q5
q6
q7
q8

закодировать внутренние состояния, допустив некритические состязания элементов памяти.

Решение. Выполним кодировку состояний. Граф последовательности кодирования показан на рисунке

2 3 4 6 7

1

8 5

Анализ кодировки показывает, что имеет место несоответствие, возникшее между состояниями q3 и q5, которые являются смежными по переходам, а их коды отличаются двумя переменными вместо желаемой одной. То же самое можно сказать относительно состояний q6 и q5. Для устранения этого недостатка кодирования изменим таблицу переходов соответствующим образом, допустив не критические состязания элементов памяти, т.е. из состояния q3 можно перейти в состояние q5 через состояние q2 и тогда разница в коде будет равна 1, что и требуется. Аналогично поступаем с q6 заменив в нем состояние q5 на q7. Результат прослеживается на измененной таблице переходов автомата

	a1	a2	a3
q1
q2
q3	2*
q4
q5
q6	7*
q7
q8

Рассмотрим другой способ, предусматривающий введение дополнительной вершины. Для этого обратимся к графу состояния исходного автомата, который примет следующий вид

001 011

000 1 a2 2 a3 3 a1 9

a3 a1 a1 a2 a1

100 8 a2 4 010

a3

101 5 a3

a1 a1

111 7 a2 6 110

a1

Как видно из рисунка, переход из q3 в q5 по a1 может быть заменен переходами по a1 из q3 в дополнительную вершину q9 и из q9 в q5. Аналогичные действия можно провести и в отношении замены перехода по a1 из q6 в q5 переходами из q6 в q7 и из q7 в q5.

Определение. Число внутренних переменных кода, изменяющих свои значения при переходе автомата из одного состояния в другое, называется расстоянием по Хеммингу между этими кодами.

В большинстве случаев необходимо так закодировать внутренние состояния, чтобы обеспечить устойчивую работу автомата и наибольшее быстродействие при заданной надежности, наименьшем объеме памяти и простой комбинационной схеме. Однако эта задача настолько сложна, что до настоящего времени не удалось получить комплексного ее решения.

Наименьшее число переменных необходимых для кодирования синхронного автомата с N внутренними состояниями определяется по формуле:

n =] log₂ N [,

где скобки ] [ обозначают операцию взятия ближайшего сверху целого числа.

Чем меньше внутренних переменных изменяется при каждом переходе, тем проще реализуется функция переходов. В силу этого вариант размещения состояний автомата может выполняться в соответствии с критерием минимальности расстояния по Хеммингу по всем переходам. Суть такого размещения заключается в максимально возможном использовании соседних кодов. Такой способ кодирования избыточен и может потребовать

n = 2 · ] log₂ N [ - 1

кодируемых переменных.

Пример. Для автомата, заданного таблицей переходов:

	x0	x1	x2	x3	x4	x5	x6	x7	Код
r0								r1
r1					r12	r11
r2							r11
r3	r4			r5
r4		r0
r5								r0
r6						r7		r9
r7		r8
r8						r2
r9		r10
r10						r2	r11
r11
r12	r0						r6	r3

выполнить кодировку внутренних состояний, используя код минимальной длины.

Решение. При кодировании соседними кодами может возникнуть ситуация, когда все соседние коды уже заняты, а состояния еще не закодированы. Такая ситуация требует увеличения расстояния по Хеммингу на следующем шаге кодирования. Такой подход к кодированию показан в столбце «код», присоединенном к таблице переходов автомата. Направление кодировки может быть прослежено на следующем графе:

r0 r1 r11

r12 r6 r7 r8

r4

r5 r3 r9 r10 r2

Оказалось, что из 18 возможных переходов 15 являются соседними с расстоянием 1; два перехода имеют расстояние 2, а один переход с r10 на r2 имеет расстояние 3. Суммарное расстояние по Хеммингу для 18 переходов равно 22. Возможно, что существует и другое более эффективное решение. Рекомендуется делать несколько вариантов кодирования, из которых отбирается лучший вариант в смысле минимальности функционала Махаланобиса:

,

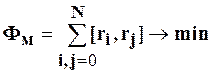где i £ j, N - число состояний. Через [r_i, r_j ] обозначено расстояние между кодами r_i и r_j по Хеммингу.