Работа с символьными выражениями

До сих пор в данной главе рассматривались примеры логических программ, работающих с натуральными числами, списками и бинарными деревьями. Однако программирование имеет более широкую область применения. В этом разделе приводятся четыре примера рекурсивных программ – программа описания многочленов программа символьного дифференцирования, программа решения задачи о ханойской башне и программа проверки выполнимости булевой формулы.

Первый пример – программа, распознающая многочлены от переменной X. Многочлены определяются индуктивно. Как сама переменная X, так и любая константа являются многочленами от X. Сумма, разность и произведение многочленов от X являются многочленами от X. Многочленами также являются результаты возведения многочлена в целую степень и деления многочлена на ненулевую константу.

Примером многочлена от x служит х² – Зх+2. Данное утверждение следует из того, что это выражение есть сумма х² – Зх и 2, принадлежность х²–Зх множеству многочленов устанавливается рекурсивно. Записав в требуемой форме приведенные выше неформальные правила, мы получим логическую программу, распознающую многочлены. Программа 3.28 задает отношение polynomial (Expression, X), истинное, если выражение Expression есть многочлен от переменной X. Приведем декларативное понимание двух правил программы. Факт polynomial (Х,Х) утверждает, что сам терм Х есть многочлен. Правило

polynomial (Term1 + Term2, Х) ¬

polynomial (Term1, X),polynomial (Term2, X).

утверждает, что сумма Term1 + Term2 есть многочлен от X, если Term1 и Term2 – многочлены от X. Дополнительными соглашениями, принятыми в программе 3.28, являются использования одноместного предиката constant для распознавания констант и бинарного функтора “­” для обозначения возведения в степень. Терм Х ­ Y обозначает X.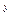

polynomial(Expression.X)

выражение Expression является многочленом от X.

polynomial(X,X).

polynomial(Term,X) ¬

constant(Term).

polynomial(Terml +Term2,X) ¬

polunomial(Term I,X), polunomial(Term2,X). polynomial(Terml –Term2, X) ¬

polynomial(Term 1,X), polynomial(Term2,X). polynomial(Term1 * Term2, X) ¬

polynomial(Term1,X,) polynomial(Term2,X). polynomial(Terml/Term2,X) ¬

polynomial(Term 1,X), constant(Term2).

polynomial(Term ­ N,X) ¬

natural_number(N),polynomial(Term,X).

Программа 3.28. Распознавание многочленов.

Следующий пример – программа нахождения производной. Реляционной схемой будет derivative (Expression.X,Diff Expression). Подразумеваемое значение – выражение Diff Expression есть производная выражения Expression по переменной X.

Как и в случае программы распознавания многочленов, логическая программа дифференцирования – просто набор соответствующих правил дифференцирования, записанный в корректном синтаксисе. Например, факт

derivative(X,X,s(0)).

означает, что производная Х по Х есть1. Факт

derivative (sin (X), X, соs (X)).

означает, что производная sin(X) по Х есть cos(X). Мы могли бы использовать и обычную математическую запись.

Типичный набор функций и их производных описан в программе 3.29.

Derivative(Expression.X, DiffExpression)

DiffExpression –- производная выражения Expression по X.

derivative(X,X,s(0)).

derivative(X ­ s(N),X,s(N) * X ­ N).

derivative(sin(X),X,cos(X)).

derivative(cos(X),X, sin(X)).

derivative(e ­ X,X,e ­ X).

derivative(log(X),X,l/X).

Программа 3.29. Правила дифференцирования..

derivative(F + G,X,DF + DG)¬-

derivative(F,X,DF),derivative(G,X,DG).

derivative(F - G,X,DF - DG) ¬

derivative(F,X,DF),derivative(G,X,DG). derivative(F“G,X,F*DG + DF*G) ¬

derivative(F,X,DF),derivative(G,X,DG).

derivative(1/F.X,-DF/(F*F)) ¬

derivative(F,X,DF).

derivative(F/G,X,(G*DF - F*DG)/(G*G)) ¬

derivative(F,X,DF),derivative(G,X,DG).

Программа 3.29. (Продолжение).

Сумма и произведение термов дифференцируются согласно соответствующим правилам для суммы и произведения. Правило дифференцирования суммы утверждает, что производная суммы есть сумма производных. Соответствующее предложение выглядит так:

derivative (F + G,X,DF + DG) ¬

derivative (F, X, DF), derivative(G, X, DG).

Правило дифференцирования произведения чуть сложнее, но и здесь логическое предложение точно следует математическому утверждению:

derivative(F*G,X,F*DG + DF*G) ¬

derivative(F, X, DF), derivative (G, X, DG).

В программе 3.29 имеются также правила дифференцирования обратной величины и дифференцирования отношения.

Правило дифференцирования сложной функции представляет несколько более тонкий случай. В правиле утверждается, что производная от f(g(x)) no x есть производная f(g (х)) по g (х), умноженная на производную g (х) по x. В данной форме правило использует квантор по функциям и находится вне области логического программирования, рассматриваемой нами.

Для каждой конкретной функции, однако, мы можем написать нужный вариант правила. Мы дадим в качестве примера правило дифференцирования Х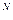и sin(X):

derivative(U­s(N),X,s(N)*U­N*DU) ¬derivative(U,X,DU). derivative(sin(U),X,cos(U)*DU) ¬ derivative(U,X,DU).

Трудности формализации правила дифференцирования сложной функции объясняются нашим выбором представления термов. Обе программы – 3.28 и 3.29 – используют “естественное” математическое представление термов, при котором терм представляет сам себя. Такой терм, как sin(X), представляется с помощью унарного функтора sin.Если выбрать другое представление, например unary_term(sin,X)в котором имя структуры стало доступно, то проблема с правилом дифференцирования сложной функции будет снята. Правило может быть сформулировано следующим образом:

derivative(unary_term(F,U),X,DF*DU) ¬

derivative(unary_term(F,U),U,DF).derivative(U,X, DU).

Отметим, что при такой записи термов все правила программы 3.29 должны быть переформулированы в терминах нового способа представления, при этом выглядеть они будут менее естественно.

Люди считают автоматическое упрощение выражений при дифференцировании само собой разумеющимся. В программе 3.29 упрощение отсутствует. Ответом на вопрос derivative (3*Х + 2,X,D)? будет D = (3*1 + 0*Х) + 0. Мы могли бы упростить D до числа 3, но это не предусмотрено в логической программе.

Следующий пример – задача о “ханойской башне” – обычный начальный пример применения рекурсии. Задача состоит в перемещении башни из п дисков с одного стержня на другой, с использованием вспомогательного диска. Перемещения осуществляются в соответствии с двумя правилами: за один раз можно перенести лишь один диск, и больший диск нельзя устанавливать на меньший.

Имеется легенда, связанная с этой задачей. Где-то в окрестностях Ханоя который во времена появления легенды был уединенным городком, спрятан монастырь. Монахи выполняют там работу, возложенную на них Богом при создании мира, решают описанную выше задачу с 3 золотыми стержнями и 64 золотыми дисками. В момент завершения работы мир должен рассыпаться в прах. Поскольку оптимальное решение задачи с п дисками требует 2ⁿ–1 перемещений нам не следует терять сон из-за подобной перспективы. Величина числа 2⁶⁴ достаточна для сохранения спокойствия.

Реляционная схема решения задачи – hanoi(N, А, В, С, Moves). Отношение истинно если Moves – последовательность перемещений для переноса башни из п дисков со стержня А на стержень В с использованием промежуточного стержня С. Это является некоторым обобщением обычного решения, при котором последовательность перемещений не вычисляется, а, скорее, выполняется. Запись перемещений использует бинарный функтор to, применяемый в виде инфиксного оператора. Терм Х to Y означает, что верхний диск со стержня Х переносится на стержень Y. Программа, решающая задачу, – программа 3.30.

hanoi(N,A,B,C. Moves) ¬

Moves – последовательность перемещений при решении задачи о ханойской башне с N дисками и тремя стержнями – А, В и С.

hanoi(s(0),A3,C,[A to В]).

hanoi(s(N),A,B,C,Moves) ¬

hanoi(N,A,C,B,Msl),

hanoi(N,C,B,A,Ms2),

append(Msl,[A to В | Ms2],Moves).

Программа 3.30. Ханойская башня.

Декларативное понимание основы решения – рекурсивного правила программы 3.30, следующее: “Moves есть последовательность перемещений s(N) дисков со стержня А на стержень В с использованием промежуточного стержня С, если Ms1 – последовательность, решающая задачу перемещения N дисков с А на С с промежуточным диском В, Ms2 последовательность, решающая задачу перемещения N дисков с C на B с промежуточным диском А, и Moves есть результат присоединения [AtoB\Ms2] к Ms1”.

Рекурсия обрывается при перемещении одного диска. Более изящен, но менее очевиден базис рекурсии, состоящий в перемещении в отсутствие дисков.Соответствующий факт:

hanoi(0,A,B,C,[ ]).

Заключительный примеротносится к булевым формулам.

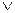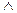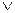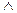Булева формула есть терм, определяемый следующим образом: константы true и false - булевы формулы; если Х и У булевы формулы, то Х У, Х У и ~ Х – булевы формулы, здесь и – бинарные инфиксные операторы дизъюнкции и конъюнкции, а ~ – унарный префиксный оператор отрицания. Булева формула F истинна, если:

F = 'true'

р==Х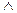Y,Х и Y истинны

F == Х 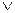Y, одна из формул Х или Y (или обе) истинны

F = ~ X, Х ложна.

Булева формула F ложна, если

F = 'false'

F = Х 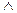Y, одна из формул Х или Y (или обе) ложны

F=X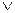Y,X и Y ложны

F = ~ X, Х истинна.

Программа 3.31 представляет собой логическую программу, определяющую истинность и ложность булевой формулы. Так как она может использоваться в случае булевой формулы с переменными, то эта программа важнее, чем кажется на первый взгляд. Булева формула с переменными выполнима, если существует истинный пример формулы. Она опровержима, если существует ложный пример. Эти отношения и вычисляются в программе.

satisfiable(Formula) ¬

Существует истинный пример булевой формулы Formula.

satisfiable(true).

satisfiable(X 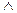Y) ¬ satisfiable(X), satistiable(Y). satisfiable(X 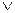Y) ¬ satisfiable(X).

satisfiable(X 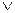Y) ¬ satisfiable(Y).

satisfiable(~ X) ¬ invalid(X).

Invalid(Formula) ¬-

Существует ложный пример булевой формулы Formula.

invalid(false).

invalid(X 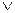Y) ¬ invalid(X), invalid(Y). invalid(X 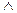Y) ¬ invalid(X).

invalid(X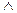Y) ¬ invalid(Y).

invatid(~ Y) ¬ satisfiable(Y).

Программа 3.31. Выполнимость булевых формул.