Оценка пригодности модели и обработка результатов экспериментов

Оценка адекватности результатов имитационного моделирования естественно может быть проведена только в тех случаях, когда имеются либо результаты аналитического моделирования, либо результаты, полученные на натурном объекте. Наиболее часто проводят сравнение средних значений методом построения доверительных интервалов. Так как средние значения при имитационном моделировании находятся сложением достаточно большого количества случайных чисел, то для их представления можно использовать нормальный закон на основании центральной предельной теоремы вероятностей. Она утверждает, что сумма достаточно большого количества случайных чисел, выработанных при достаточно общих условиях, подчинена нормальному закону вне зависимости от того, какому закону подчинены сами случайные числа, при этом 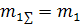, а 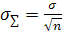. Поэтому для оценки математических ожиданий, вычисляемых на основе суммирования случайных чисел, можно построить доверительный интервал на основании нормального закона, так, как это показано на рисунке 14:

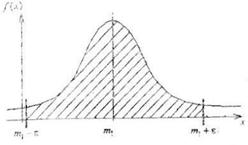
Рисунок 14. Доверительный интервал для оценок математических ожиданий, построенный на основании их подчинения нормальному закону

Для оценки адекватности выполняются следующие действия:

1. Задаемся доверительной вероятностью .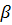

Рекомендуемое значение 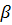=0,95. По статистическим таблицам находим 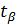, которое для рекомендуемого значения 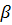=0,95 равно 1,96.

2. Задаемся количеством проводимых экспериментов .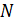

Рекомендуемое значение .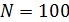

3. Задаемся количеством реализаций в каждом эксперименте .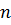

Рекомендуемое значение .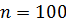

4. Проводим 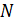экспериментов, каждый из которых состоит из 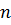реализаций.

По результатам моделирования находятся оценки математического ожидания 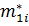, 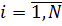и стандартного отклонения , .

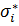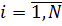5. Вычисляем половину ширины доверительного интервала: .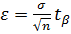

В качестве 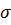берется стандартное отклонение, вычисленное либо по аналитической модели, либо по результатам экспериментов на натурном объекте, в зависимости от того, с чем проводится сравнение. Если по результатам аналитического моделирования вычислить стандартное отклонение не представляется возможным, то вместо него используют его оценку, вычисленную как среднее значение по 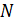проведенным экспериментам: .

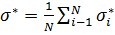6. Подсчитываем количество попаданий оценок математических ожиданий в доверительный интервал по выполнению условия:

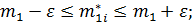
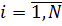. В качестве 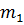берется математическое ожидание, вычисленное при аналитическом моделировании, либо его оценка, найденная по результатам натурного эксперимента. Если количество попаданий оценок математических ожиданий в доверительный интервал не меньше 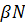, то имитационную модель считаем пригодной по тесту адекватности.

Для оценки устойчивости результатов имитационного моделирования выполняются следующие действия:

1. Задаемся доверительной вероятностью .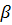

Рекомендуемое значение 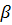=0,9. По статистическим таблицам находим 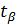, которое для рекомендуемого значения 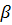=0,95 равно 1,96.

2. Задаемся количеством проводимых экспериментов – .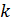

Рекомендуемое значение 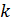=15, тогда количество сочетаний из количества экспериментов 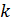=15 по два сравниваемых экспериментов эксперимента 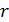=2 составит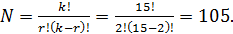

3. Задаемся количеством реализаций в каждом эксперименте .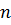

Рекомендуемое значение 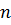=100.

4. Проводим 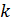экспериментов, в каждом из которых проводится по 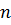реализаций.

По результатам моделирования находятся оценки математического ожидания 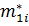, 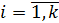и стандартного отклонения , .

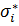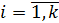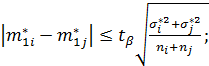
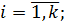
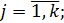
5. Подсчитываем количество случаев выполнения условия сравнения результатов проведенных экспериментов по неравенству: 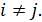(3)

6. Если количество случаев выполнения условия (3) не меньше, то имитационную модель считаем пригодной по тесту устойчивости. Это означает, что результаты имитационного моделирования несущественно зависят от используемых последовательностей случайных чисел.

Для оценки значимости результатов имитационного моделирования от изменения факторов, отобранных для моделирования, рекомендуется использовать дисперсионный анализ. При проведении дисперсионного анализа требуется выполнение следующих требований:

1. Независимость последовательностей используемых случайных чисел, что обеспечивается применением качественных генераторов случайных чисел.

2. Равенство генераторов во всех проводимых экспериментах, для чего рекомендуется в каждом варианте плана проводить одинаковое количество экспериментов с одинаковым количеством реализаций во всех проводимых экспериментах.

3. Нормальность сумм результатов на основании центральной предельной теоремы теории вероятностей.

Для проведения дисперсионного анализа требуется выполнить следующие действия:

1. Изменяя анализируемый фактор 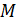по градациям, провести в каждой точке плана по 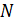экспериментов, в каждом из которых выполнять по 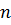реализаций и получить оценки математических ожиданий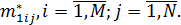

2. Зададимся уровнем значимости критерия Фишера.

Рекомендуемое значение

3. По статистическим таблицам находим критическое значение критерия Фишера 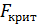, при двух степенях свободы 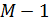и 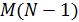, и уровне значимости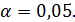

4. Вычисляем критерий Фишера по формуле: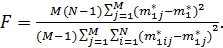

5. Если вычисленное значение критерия Фишера не меньше критического, то делаем заключение, что изменение проанализированного фактора существенно влияет на изменение результативного показателя, и, таким образом, модель признается пригодной по тесту оценки значимости.

При проведении экспериментов рекомендуется подбирать переменные, участвующие в экспериментах так, чтобы они были случайными, количественными и непрерывными. В этом случае для обработки результатов рекомендуется применять регрессионный анализ, обладающий свойствами сравнительной простоты и конструктивности, которые позволяют использовать регрессионные уравнения для генерации эффективных решений на основе оптимизационных методов.

Регрессионный анализ основан на методе наименьших квадратов, который требует, чтобы сумма квадратов отклонений экспериментальных значений от вычисленных по аппроксимирующей зависимости была минимальной:

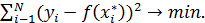
Если часть переменных количественная, а часть качественная, то рекомендуется применять корреляционный анализ. Корреляция – это взаимозависимость случайных величин между собой. В качестве количественной меры оценки взаимосвязи между случайными величинами используется коэффициент линейной корреляции.

В случае если значение коэффициента линейной корреляции, вычисленное по формуле 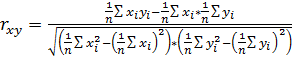, по модулю не меньше 0,8, то можно ожидать наличие между переменными линейной зависимости и в уравнения регрессии вводить сами факторы в первой степени. Если лежит в диапазоне от критического значения до 0,8, то в уравнения регрессии рекомендуется вводить сравнительно несложные функции от факторов. Если меньше критического значения, то такие факторы рекомендуется не включать в уравнения регрессии.

Если переменные не количественные, а качественные, то рекомендуется использовать дисперсионный анализ. Он основан на разложении общей изменчивости результативного показателя (общей дисперсии) на объясненную дисперсию, которую удалось объяснить изменением переменных, вошедших в уравнение регрессии, и остаточную регрессию, которую объяснить не удалось.