Метод моментов для равномерного закона

Непрерывная случайная величина 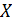имеет равномерное распределение на отрезке 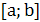, если ее функция плотности постоянна на этом отрезке и равна 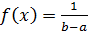при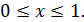

На рисунке 9 приведены функция распределения 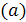и функция плотности равномерного закона распределенных случайных чисел на отрезке [0;1]:

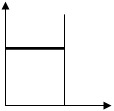
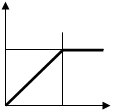F(x) f(x)

0 1 x 0 1 x

Рисунок 9.

Первый и второй начальные моменты:

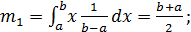
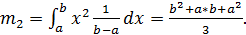
Стандартное отклонение и параметры равномерного закона:

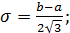
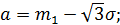
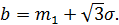
Вычислим вероятность попадания случайной величины в интервалы гистограммы и гипотетическую функцию распределения:

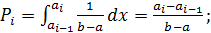
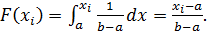
Следует учитывать, что при построении гистограммы принимается: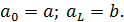

Пример 3. Аппроксимация экспериментального распределения случайных чисел равномерным законом с оценкой качества аппроксимации по критерию согласия Колмогорова.

Экспериментальное распределение представляет собой выборку, состоящую из 10 трехразрядных чисел, поэтому проведем аппроксимацию с оценкой качества аппроксимации по критерию Колмогорова. Представим распределение случайных чисел по возрастанию их значений: 137, 221, 353, 366, 367, 507, 686, 905, 918, 985 и построим по нему эмпирическую функцию распределения, представленную на рис. 10:

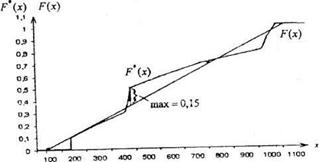
Рисунок 10. Эмпирическая и гипотетическая функции распределения

Вычислим основные характеристики эмпирического распределения:

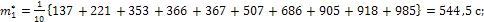
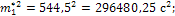
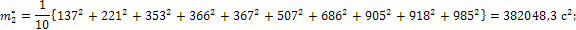
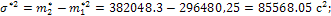
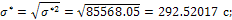
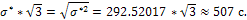
Вычислим параметры равномерного закона:

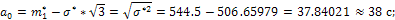
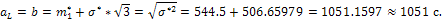
По двум найденным точкам построим прямую линию, которая является гипотетической функцией распределения. По рисунку 10 находим, что максимальная разница между эмпирической и гипотетической функцией распределения при аргументе, равном 367. Уточним значение функцией распределения для этого значения и вычислим критерий согласия Колмогорова:

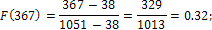
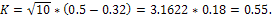
По статистическим таблицам находим коэффициент доверия высказанной гипотезе: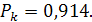

Вывод: имеющиеся статистические данные не противоречат гипотезе о их подчинении равномерному закону по критерию согласия Колмогорова.

Пример 4. Аппроксимация экспериментального распределения 100 одноразрядных чисел равномерным законом с оценкой качества аппроксимации по критерию согласия Пирсона.

Выборка из 100 случайных чисел представлена в виде совокупности, состоящей из 5 строк и 20 столбцов:

Подсчитаем количество символов каждого типа и построим гистограмму, представленную на рисунке 11:

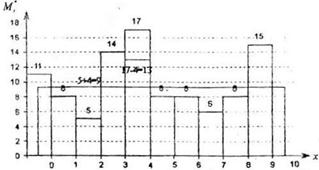
Рисунок 11. Гистограмма распределения 100 одноразрядных случайных чисел

Вычислим основные статистические характеристики распределения, параметры закона, значение критерия Пирсона и по статистическим таблицам определим коэффициент доверия выдвинутой гипотезе:

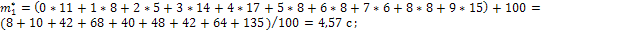
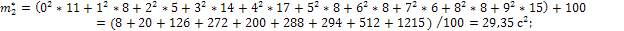
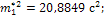
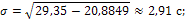
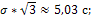
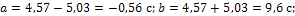
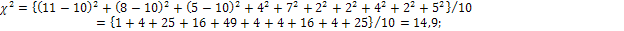
Вывод: ввиду того, что найденный коэффициент доверия не укладывается в рекомендуемый 10%-й доверительный интервал, то гипотезу отвергаем.