2014-02-02
804
Временная когерентность определяется разбросом значений частот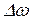 
и соответственно значений модуля волнового вектора 
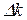(так как 
).
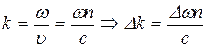Пространственная когерентность обусловлена разбросом направлений вектора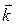 
из-за наличия протяженного источника света. Рассмотрим на примере диска. Угол 
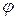, под которым виден диск в данной точке и характеризует разброс напр-ий вектора 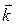. (Считаем, что временная когерентность достаточная для получения четкой интерференции картины).
Если излучение от диска падает на две щели, то волны идущие по направлению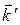 
создают первый максимум 
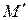выше на 
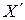, чем по направлению волны 
.
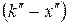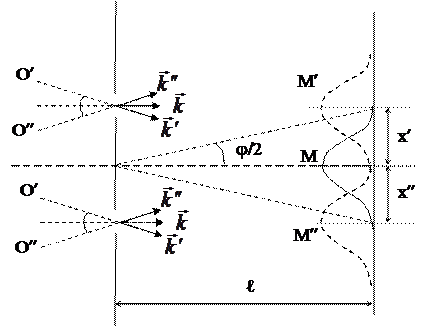Смещение 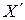будет меньше, чем ширина интерф. полосы 
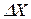, то максимумы практически наложатся друг на друга и источник можно считать точечным. Интереферентная картина наблюдается. Если 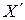~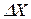максимумы наложатся на соседние минимумы и интерф-ой картины не наблюдается. Т.о. интерфер. картина наблюдается при услови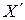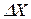и <или
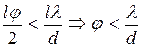
Это условие можно записать для расстояния между щелями
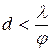(3.7)
При уменьшении d – расстояния между щелями или точками волновой поверхности можно добиться соблюдения (3.7). Колебания между точками монохроматической волновой поверхности можно считать когерентными, если расстояние между ними меньше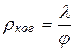 
- называется радиусом когерентности. Лазер обладает большой пространственной и временной когерентностью. Томас Юнг в 1802 году увеличил пространственную когерентность, пропустив свет сначала через одно отверстие в ширме, а потом через два – в другой ширме.
При увеличении расстояния от источника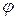 
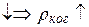, то есть пространственная когерентность увеличивается.
