2014-02-02
976
Временная когерентность. Любая световая волна является наложением колебаний всевозможных частот. Даже для света, который считается монохроматическим, колебания заключены в конечном интервале частот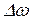 
(или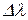 
). Кроме того, фаза и амплитуда испытывают случайные (хаотические) изменения. Поэтому в общем случае волна описывается уравнением
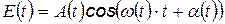
Посчитаем для простоты, что А не зависит от t. Введем среднее значение частоты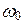 
- относительно которого происходят изменения 
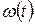. Тогда фазу можем записать в виде
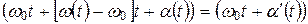
Обозначим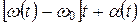 
через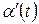 
.
То есть мы получили функцию, у которой хаотические изменения претерпевает лишь фаза. Если происходит сложение двух волн с преобразованными, как сделано выше, фазами, то результирующая интенсивность, как известно из (3.1)’, будет зависеть от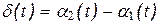 
.
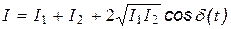
то есть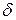 
- разность фаз будет не постоянной, а зависеть от времени.
Если за время срабатывания прибора (глаз ~ 0.1 с) tприб. Значения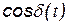 
менялись от +1 до –1, то интерферентную картину не зарегистрируем и 
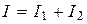. Если 
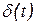за время tприб., то волны будем считать когерентными, и интерф. картина регистрируется. Можно ввести время когерентности. Это время tког., за которое случайное изменение фазы достигает значения p. При постоянной времени прибора
tприб >> tког – интерфер. картина на наблюдается,
tприб<< tког – наблюдается. (3.6)
Расстояние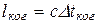 
, на которое смещается волна за время tко, называется длиной когерентности. Расстояние, на которое фаза меняется на ~ p.
При разности хода лучей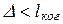 
- интерфер. картина наблюдается (для разделенных волн).
