Зоны Френеля

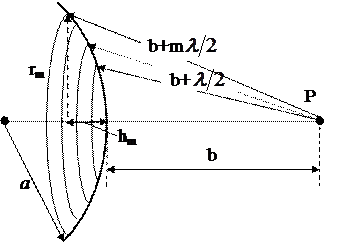
Френелем был предложен метод зон Френеля, которые позволят рассчитывать амплитуду простым алгебраическим суммированием. По выражению (4.1) рассчитывать очень сложно. Этот метод удобен в случаях симметричного распространения световых волн. Рассмотрим на примере сферической волны от точ. источника S. Найдем амплитуду в точке Р. Световые волны симметричны относительно SP.

Суть метода зон Френеля состоит в разбиении волновой поверхности на кольцевые зоны, расстояние от краев соседних зон до Р отличаются на 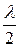. Следовательно, результирующие колебания, создаваемые каждой из зон в целом, для соседних зон будут отличаться по фазе на p (то есть в противофазе).

Рассчитаем площади зон

Площадь зоны m

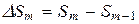
- площади сферических сегментов ().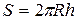

Из рисунка

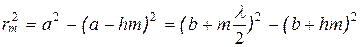
r_m – радиус внешней границы

h_m – высота сегмента

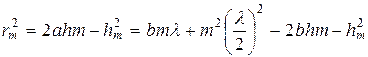(4.2)

При небольших m слагаемым 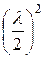пренебрежем.

(4.3)

Тогда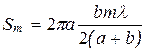

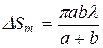
Так как 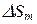не зависит от m, то при небольших m площади зон примерно одинаковы.

При малых m 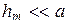и в выражении (4.2) членом пренебрежем

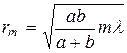(4.4)

Если положить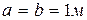

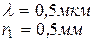
Так как 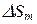уменьшается при увеличении m, то амплитуда возбуждается зоной в точке Р с увеличением m убывает.

Так как колебания от зон приходят в противофазе, то результат амплитуды:

Если ее записать как

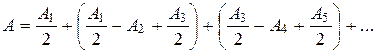
и положить, что

то

Таким образом, амплитуда, создаваемая сферической волной в точке Р. равна половине амплитуды, создаваемой первой зоной Френеля. Если в экране оставить отверстие под 1 зону Френеля, то амплитуда будет А₁, то есть в 2 раза больше, чем А. А интенсивность в 4 раза будет больше.

Если перекрыть все четные или нечетные зоны Френеля, то интенсивность в точке Р резко возрастает. Такая платинка называется зонной. Есть фазовая зонная платинка, которая изменяет фазу, допустим, нечетных зон Френеля на 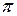. Усиление интенсивности в 4 раза (амплитуда в 2 раза).