Источники коммерческого права РФ и коммерческое законодательство

.

Подключая фильтр в единую схему с си­стемой, получаем эквивалентную передаточную функ­цию

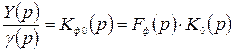. (8.76)

В результате любой стационарный случайный процесс можно представить эквивалентным ему процессом на выходе формирующего фильтра при воздейст­вии на его вход белого шума. Такое представление ре­ального сигнала облегчает определение СКО, так как позволяет анализировать САУ методами для входного белого шума.

8.9.2. Расчет флуктуационных ошибок и ошибок

от задающих воздействий

Предположим, что на вход системы (рис.8.12) поступает помеха f(t), а полезный сигнал x(t)=0. Требуется определить флуктуационную ошибку, вызываемую отработкой системы помехи на ее входе. Спектральная плотность помехи равна 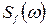. Передаточная функция системы известна.

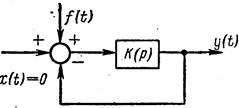
Рис. 8.12. К определению флуктуационной ошибки

Поскольку в этом слу­чае весь сигнал на выходе системы представляет со­бой сигнал ошибки, спект­ральная плотность ошибки равна

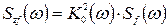, (8.77)

где 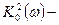квадрат амплитудно-частотной характеристики замкнутой системы.

Для облегчения вычисления интеграла (8.74) и при­ведения его к табличному спектральную плотность вход­ного сигнала представляем в виде

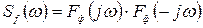. (8.78)

Подставляя (8.78) в (8.77) и обозначая 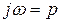, полу­чим

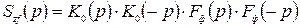. (8.79)

Обычно К₀(Р) — рациональная дробь, 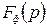также может быть представлено в виде рациональной дроби.

Учитывая (8.72) и (8.74), получим выражение для среднего квадрата ошибки в виде табличного интеграла:

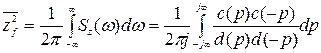, (8.80)

где многочлены под интегралом

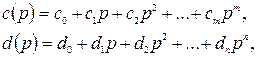
причем .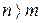

Таблицы интегралов до п = 6 приведены в литературе [9].

Если помеха действует не на входе системы, то вме­сто К₀(р) берется передаточная функция K_yf(p), соот­ветствующая месту приложения воздействия f.

Рассмотрим более общий случай, когда на систему помимо задающего воздействияx(t) действует одновременно помеха f(t)/

Суммарная ошибка

.

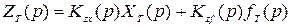Спектральная плотность ошибки

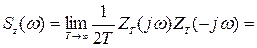
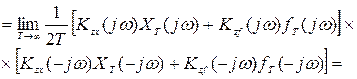
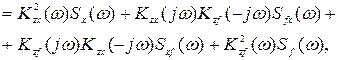(8.81)

где

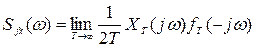
и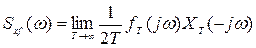

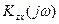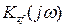представляют собой взаимные спектральные плотности полезного сигнала и помехи, а и — ча­стотные характеристики ошибки от полезного сигнала и помехи. При отсутствии корреляции между полезным сигналом и помехой

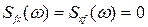
и формула (8.81) упрощается:

. (8.82).

Для помехи, приложенной совместно с задающим воздействием, когда 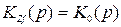и при отсутствии корреляции между ними получим

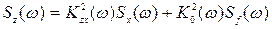(8.83).

Средний квадрат ошибки

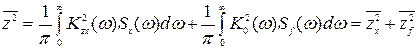, (8.84)

где

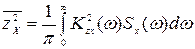(8.85)

- составляющая дисперсии ошибки, вызываемая задающим воздействием ;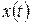

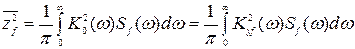(8.86)

- составляющая дисперсии ошибки, вызываемая возмуща­ющим воздействием f(t).

Среднеквадратическое значение суммарной ошибки системы

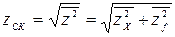. (8.87)

Среднеквадратическую ошибку системы, определяе­мую по формуле (8.87), не следует смешивать со среднеквадратическим отклонением 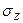, которое равно положи­тельному квадратному корню из дисперсии .

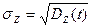Как следует из формулы (8.84) среднее значение квадрата ошибки зависит от структуры системы (вида ее передаточной функции и параметров) и от спектраль­ных плотностей входного сигнала и помехи.

Для минимизации соответствующей составляющей ошибки системы необходимо уменьшать площадь под кривой произведения спектральной плотности входного сигнала на квадрат амплитудно-частотной характери­стики.

Заменяя в выражении (8.85) передаточную функцию ошибки на передаточную функцию замкнутой системы K₀(p), получим средний квадрат выходной величины .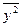

Если в задающем сигнале x(t) можно выделить воз­действие в виде неслучайной составляющей m_x(t), пред­ставляющей собой медленно меняющуюся функцию вре­мени, и стационарный центрированный случайный про­цесс, т. е.

,

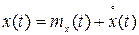то точность системы можно оценить средним квадратом ошибки, равным сумме квадратов динамической и слу­чайной ошибок:

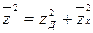
или

.

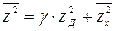Здесь 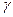— коэффициент, определяющий удельный вес ди­намической ошибки;

,

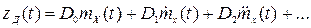где D₀, D₁,D₂,... — коэффициенты ошибки.

Для случая, когда можно предположить, что скорость изменения задающего воздействия постоянна в течение рассматриваемого интервала времени, т. е. 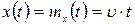, а помеха - белый шум, в соответствии с (8.84) по­лучим для систем с астатизмом 1-го порядка

.

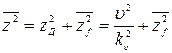Пример. Определить средний квадрат суммарной ошибки САУ с передаточной функцией 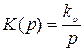, если на входе системы действует задающее воздействие со спектральной плотностью 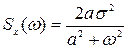и помеха со спектральной плотностью 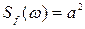. Ошибка системы определяется формулой (8.84). Вторая доставляющая ошибки уже была определена.

.

Вычислим первую составляющую ошибки (от задаю­щего воздействия).

Передаточная функция ошибки

.

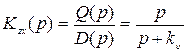Представим спектральную плотность через сопряжен­ные составляющие:

.

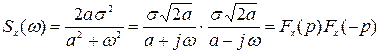Находим

.

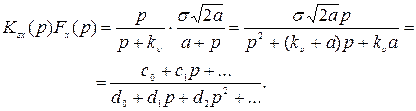Табличный интеграл

.

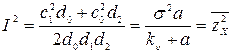Окончательно получим

.

Из данного выражения следует, что для уменьшения составляющей ошибки от полезного сигнала необходимо увеличение 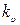, а для уменьшения составляющей ошибки от помех 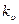нужно уменьшать.

Основным достоинством аналитического метода яв­ляется возможность установления связи между величи­ной СКО и параметрами системы, что позволяет опреде­лять значения параметров системы, при которых СКО оказывается минимальной.

Лекция 30

План лекции:

1. Графоаналитический метод расчета случайных ошибок САУ.

2. Оценка флуктуационных ошибок, обусловленных широкополосными

воздействиями.

3. Расчет дисперсии помехи с помощью корреляционной функции.

4. Определение флуктуационных ошибок с помощью электронной модели

5. Рекомендуемая литература [9].

8.9.3. Графоаналитический метод расчета

В инженерной практике для систем управления высокого порядка применяют приближенный графоаналитический метод определения случайных ошибок. Его удобно применять, если спектраль­ные плотности задающего воздействия 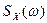и помехи 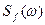и амплитудно-частотные характеристики заданы графически или описываются сложными выражения­ми. Метод является наглядным и позволяет сразу решить, как нужно изменить частотные характеристики системы, чтобы уменьшить ошибку, вызванную случайным сигна­лом.

Рассмотрим этот метод применительно к вычислению ошибки от помех.

Поскольку спектральная плотность ошибки 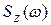функция четная, то можно записать

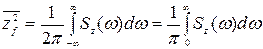. (8. 88 )

Имея в виду, что

, (8.89)

при известных передаточной функции системы 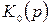и спектральной плотности стационарного случайного воз­действия на входе си­стемы 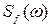можно предложить следующий порядок расчета среднеквадратической оши­бки.

1. Строится АЧХ замкнутой системы 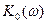(рис. 8.13). Ор­динаты этой кривой возводятся в квадрат и строится кривая .

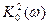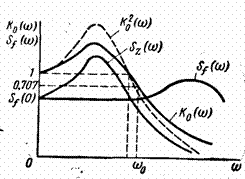
Рис. 8.13. К графоаналитическому определению флуктуационной ошибки

2. Строится кривая спектральной плотно­сти для случайного сигнала ошибки. Для этого значение спектральной плотности на входе 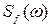умно­жается на величину квадрата АЧХ системы для каждой данной частоты.

3. Определяется значение интеграла 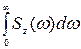. Для этого подсчитывается площадь, заключенная между кри­вой и осью абсцисс.

4. Средний квадрат ошибки в соответствии с форму­лой (8.86) определяется путем деления найденной пло­щади на 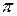, т. е.

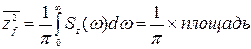. (8.90)

Среднеквадратическая ошибка вычисляется по формуле:

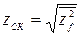. (8.91)

График спектральной плотности ошибки можно также рассчитать, пользуясь логарифмическими частот­ными характеристиками (ЛЧХ). По заданному значению К(р) определяют логарифмические амплитудно-частот­ные (ЛАЧХ) и фазо-частотные характеристики (ЛФЧХ) разомкнутой 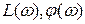системы, затем находят ЛАЧХ замкнутой системы 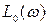, ее значения удваивают, т. е. определяют 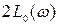. Значения 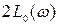суммируются с величиной 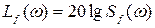. В результате получаем

.

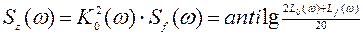Для определения ошибки поступают далее так же, как и в пп. 3 и 4.

Как видно из соотношения (8.89), флуктуационная ошибка в общем случае зависит от взаимного расположе­ния графиков 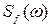и 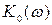(рис.8.13). При совпадении максимумов характеристик флуктуационная ошибка оказывается большой, и наоборот, разнесение этих мак­симумов выбором параметров системы приводит к умень­шению флуктуационной ошибки. Это следует учитывать при расчете САУ.

Уменьшения флуктуационной ошибки можно также добиться путем уменьшения пика АЧХ, т. е. выполнени­ем системы более узкополосной и достаточно задемпфированной (уменьшить 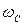– частоту среза разомкнутой системы).

8.9.4. Оценка флуктуационных ошибок, обусловленных

широкополосными воздействиями

Во многих случаях воздействие обладает широкополосным спектром и в пределах полосы пропу­скания САУ оказывается практически постоянным 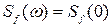(рис. 8.13). При этих условиях флуктуационную ошибку с определенным приближением можно вычислить по формуле:

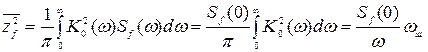, (8.92)

где 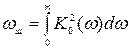- полоса шумов САУ (эффективная полоса пропускания системы). Полосу шумов 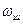можно определить аналитически, пользуясь теоремой Парсеваля:

.

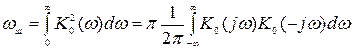Заменяя 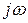на р, получим

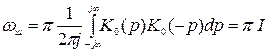, (8.93)

т. е. полоса шумов равна табличному интегралу , поли­номы числителя и знаменателя подынтегрального выра­жения которого совпадают с соответствующими полино­мами передаточной функции системы, умноженному на .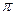

В табл. 8.1 приведены значения 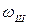для некоторых элементарных звеньев и систем, выраженные через их параметры.

Учитывая, что спектральная плотность шума S_f(0)=S_f постоянна и задана на ограниченной полосе частот от до , иногда удобно использовать определение дисперсии на выходе системы

,

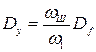где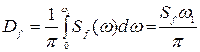- дисперсия на входе системы.

Пример 1. Определить 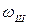системы с передаточ­ной функцией

.

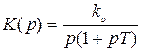Передаточная функция замкнутой системы

.

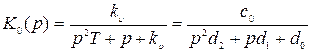Следовательно,

.

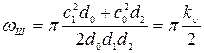Для приближенных расчетов можно положить

,

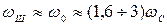где 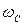— частота среза разомкнутой системы; 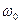— полоса пропускания замкнутой системы.

Таблица 8.1

K(p)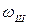

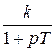
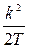
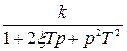
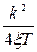
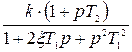
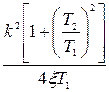
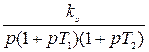
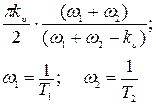
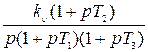
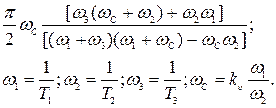
Пример 2. Рассчитать флуктуационную ошибку САУ, имеющей частоту среза 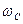= 11сек^-1 и запас по фазе 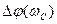=45°.

По приближенным соот­ношениям находим

.

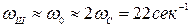Флуктуационная ошибка

.

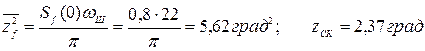Полоса шумов по формуле (8.93)

.

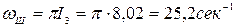Флуктуационная ошибка

.

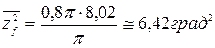Следовательно, приближенный метод расчета флуктуационной ошибки при приемлемых запасах устойчиво­сти имеет достаточную точность.

Лекция 31

План лекции:

1. Расчет дисперсии помехи с помощью корреляционной функции.

2. Вычисление среднеквадратической ошибки следящей системы.

3. Рекомендуемая литература [9].

8.9.5. Расчет дисперсии помехи с помощью

корреляционной функции

Для определения дисперсии помехи можно восполь­зоваться соотношением (8.25), согласно которому

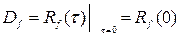. (8.94)

Если наряду с двусторонним преобразованием Фурье (8.27) и (8.29) рассмотреть односторонние преобразова­ния:

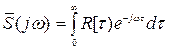, (8.95)

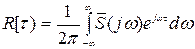, (8.96)

где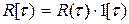 — правая полуветвь двусторонней четной корреляционной функции; 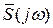— ее комплексный спектр,

то расчеты по формуле (8.94) могут быть осуществлены, как у Шаталова А. С., в области изображений на основе предельного перехода:

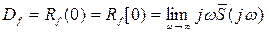(8.97)

Вследствие четности корреляционной функции 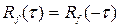и спектральной плотности 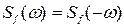между односторонним и двусторонним преобразованиями Фурье устанавливается зависимость:

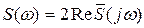, (8.98)

причем

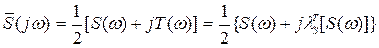, (8.99)

где 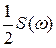— вещественная часть комплексного спектра; 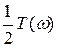— его мнимая часть; 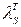— символическая запись операции опреде­ления по вещественной части комплекс­ного спектра его мнимой части.

Учитывая (8.99), формулу (8.97) можно предста­вить в виде

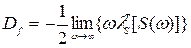(8.100)

Помимо определения одной точки корреляционной функции (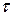=0), часто требуется нахождение полной кор­реляционной функции по ее полуветви (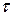>0),

т. е.

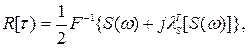(8.101)

где 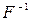— операция обратного преобразования Фурье.

Пример. Определить корреляцион­ную функцию на выходе системы при входном белом шуме единичного уровня.

Передаточная функция системы

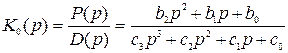(8.102)

или частотная характеристика

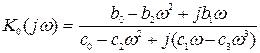. (8.103)

Учитывая, что 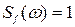, имеем

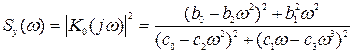(8.104)

В соответствии с (8.99) нетрудно установить, что комплексный спектр корреляционной функции на выходе системы должен иметь тот же знаменатель, что и (8.103). Поэтому

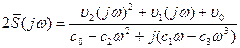(8.105)

Раскрывая соотношение (8.98), определим неизвест­ные коэффициенты :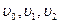

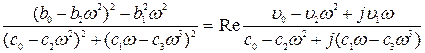(8.106)

Из (8.106) следует тождество:

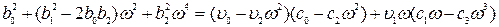(8.107)

Приравнивая коэффициенты при одинаковых степе­нях 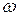в левой и правой частях тождества (8.107), полу­чаем систему уравнений:

;

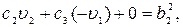
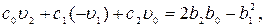
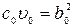откуда

,

.

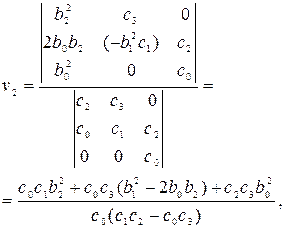
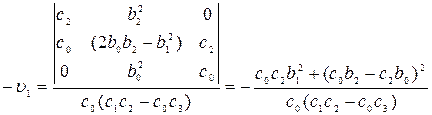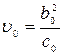Таким образом, определен комплексный спектр кор­реляционной функции (8.105). В преобразованной по Лапласу форме его можно записать как

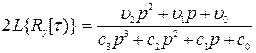
Путем обратного преобразования Лапласа находят всю правую полуветвь корреляционной функции:

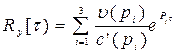
для некратных полюсов .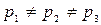

На основе предельного перехода (8.97) можно опре­делить только выходную дисперсию

.

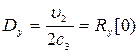Аналогичным путем можно произвести расчет выход­ной корреляционной функции при произвольной стацио­нарной помехе. При этом входная спектральная плот­ность формируется из белого шума единичного уровня некоторым формирующим фильтром с передаточной функцией 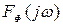, определяемой из уравнения:

.

Полученные ранее формулы для частного вида пере­даточной функции (8.102) могут быть обобщены на пере­даточную функцию произвольного порядка.

Предложенная методика преобразования корреляци­онных функций помех позволяет однотипным методом на основе одних и тех же определителей с различными заме­щенными столбцами рассчитывать не только дисперсию, но и все свойства корреляционной функции на выходе си­стемы при заданном стационарном случайном воздейст­вии. В ряде случаев это дает некоторые расчетные пре­имущества по сравнению с непосредственными расчетами по формуле (8.41) даже при использовании табличных интегралов.

8.9.6. вычисление среднеквадратической ошибки

следящей системы

Найдем среднеквадратическую ошибку следящей системы автосопровождения цели радиолока­ционной станцией. На вход системы поступает задающее воздействие 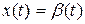(азимут цели) сов­местно с помехой f(t). Сигнал ошибки равен разности входного полезного сигнала x(t) и сигнала на выхо­де 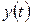(азимут антенны) следящей системы РЛС:

.

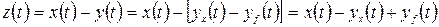Задающее воздействие и помеха — стационарные слу­чайные не коррелированные сигналы. Такой сигнал по­ступает на усилительное устройство системы. Передаточная функция разомкнутой системы

.

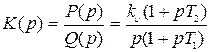Спектральная плотность ошибки

.

Задающим воздействием системы будем считать 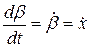. Спектральная плотность его найдена в формуле (8.50). В качестве помехи примем случайный процесс типа белого шума:

.

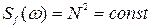Подставив в выражение спектральной плотности ошибки ее составляющие, получим:

,

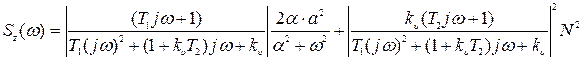где

,

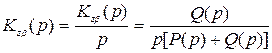т. e. среднее значение квадрата ошибки можно предста­вить в виде суммы составляющих:

.

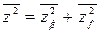Пользуясь выражением для табличного интеграла, значение квадрата СКО 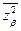найдем в виде

.

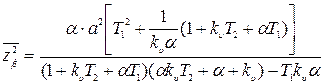Аналогично можно определить квадрат СКО:

.

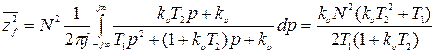Если известны параметры системы и помехи 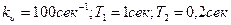, , 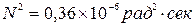то среднеквадратическая ошибка:

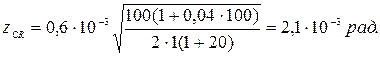
Выражения для дисперсии флуктуационной ошибки, определенной через параметры передаточной функции разомкнутой системы К(р), при постоянной величине спектральной плотности помехи на входе, системы, при­ведены в табл. 8.2.

Таблица 8.2

Передаточные функции К(р)	Дисперсия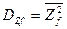

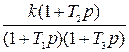
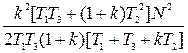
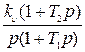
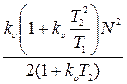
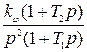
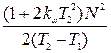
B заключение отметим, что приведенные соот­ношения для статистического анализа в частотной об­ласти удобны в установившемся режиме. Анализ во вре­менной области более сложен, но целесообразен для моментов времени, близких к моменту приложения воз­действия.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования – М.: Наука,1975. – 768 с.

2. Воронов А.А. Основы теории автоматического управления. Автоматическое регулирование непрерывных систем. –М.: Энергия, 1980. –312 с.

3. Макаров И.М., Менский Б.М. Линейные автоматические системы. Элементы теории, методы расчета и справочный материал. – М.: Машиностроение, 1982. – 504 с.

4. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1989. – 301 с.

5. Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бесекерского. – М.: Наука, 1978. – 512 с.

6. Справочник по теории автоматического управления / Под ред. А.А. Красовского. – М.: Наука, 1987. – 712 с.

7. Теория автоматического управления / Под ред. А.С.Шаталова. – М.: Высшая школа, 1977. – 448 с.

8. Техническая кибернетика. Теория автоматического регулирования / Под ред. В.В. Солодовникова. Кн.1,2,3. – М.: Машиностроение, 1967-1969.

9. Лившиц Н.А., Пугачев В.Н. Вероятностный анализ систем автоматического управления. – М.: Сов. Радио, 1963. – 896 с.

Рассмотрено на заседании

кафедры ПУ

Протокол № от 2005 г.

Зав. кафедрой ПУ__________________ В. Я. Распопов