Персептрон

Ф. Розенблатт в 1958 году ввел понятие персептрона как первой модели обучения с учителем [6]. Обучение персептрона требует наличие учителя и состоит в таком подборе весов 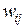,чтобывыходной сигнал 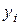был наиболее близок к заданному значению 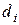. При таком способе обучения, каждой обучающей выборке, представленной вектором x поставлено в соответствии ожидаемое значение 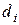на выходе i -го нейрона.

Наиболее популярный метод обучения персептрона, называемый правилом персептрона, состоит в подборе весовых коэффициентов по следующему алгоритму:

· при первоначально выбранных (как правило, случайным образом) значениях весов 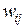на вход нейрона подается обучающий вектор x и рассчитывается значение выходного сигнала 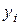. По результатам сравнения значения 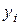с заданным значением 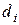уточняются значения весов;

· если 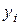совпадает с ожидаемым значением 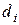, то весовые коэффициенты w_ij не изменяются;

· если 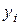=0, а соответствующее значение 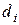=1, то значения весов уточняются по формуле 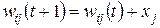, где (t+1) – это номер текущего цикла, а t – номер предыдущего цикла;

· если 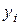=1, а соответствующее значение 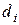=0, то значения весов уточняются по формуле 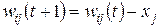, где (t+1) – это номер текущего цикла, а t – номер предыдущего цикла;

По завершении уточнения весов предоставляются очередной обучающий вектор x и связанное с ним значение 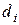, и значения весов уточняются заново. Этот процесс повторяется для всех обучающих выборок, пока не будут минимизированы различия между всеми значениями 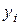и соответствующими им значениями .

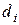Правило персептрона представляет собой частный случай (если сигналы принимают только двоичные значения 0 и 1) предложенного позже правила Видроу-Хоффа [7], используемого для подбора весов нейронов разного типа:

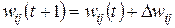, (2.5)

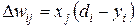. (2.6)

Аналогичные соотношения используются при подборе веса порогового элемента 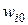, для которого входной сигнал всегда равен 1:

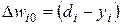. (2.7)

Минимизация различий между фактическими реакциями нейрона 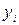и ожидаемыми значениями 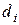может быть представлена как минимизация функции погрешности, чаще всего определяемой как минимум квадратичного отклонения:

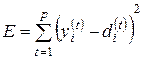, (2.8)

где p означает количество обучающих примеров (выборок). Такая минимизация для персептрона проводится по методу безградиентной оптимизации. Эффективность метода при большом количестве обучающих выборок невелика, а количество циклов обучения и длительность быстро возрастают, причем без гарантии достижения минимума целевой функции. Устранить эти недостатки можно только в случае применения непрерывной функции активации, при которой целевая функция E также становится непрерывной, что дает возможность использовать градиентные методы минимизации.