Структуру RBF- сети можно усилить путем применения масштабирования входных сигналов. Если принять во внимание, что многомерная функция может иметь различный масштаб по каждой оси, с практической точки зрения оказывается полезным уточнить норму масштабирования путем ввода в определение эвклидовой метрики весовых коэффициентов в виде матрицы Q.
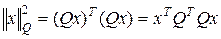 (4.31)
(4.31)
Масштабирующая матрица при N -мерном векторе x имеет вид:
 (4.32)
(4.32)
При обозначении произведения матриц 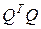 матрицей корреляции C в общем случае получим:
матрицей корреляции C в общем случае получим:
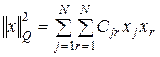 (4.33)
(4.33)
Если масштабирующая матрица Q имеет диагональный вид, то получаем 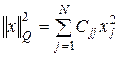 . Это означает, что норма масштабирования вектора рассчитывается согласно стандартной формуле Эвклида, с использованием индивидуальной шкалы для каждой переменной
. Это означает, что норма масштабирования вектора рассчитывается согласно стандартной формуле Эвклида, с использованием индивидуальной шкалы для каждой переменной 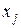 . При Q=1 взвешенная метрика Эвклида сводится к классической метрике
. При Q=1 взвешенная метрика Эвклида сводится к классической метрике 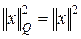 .
.
В случае использования функции Гаусса с центром в точке 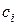 и масштабирующей взвешенной матрицы
и масштабирующей взвешенной матрицы  , связанной с i -й базисной функцией, получим обобщенную форму функции Гаусса:
, связанной с i -й базисной функцией, получим обобщенную форму функции Гаусса:
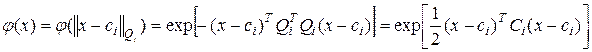 (4.34),
(4.34),
где матрица 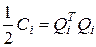 играет роль скалярного коэффициента
играет роль скалярного коэффициента 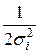 стандартной многомерной функции Гаусса, заданной выражением (4.5).
стандартной многомерной функции Гаусса, заданной выражением (4.5).
Во многих практических приложениях масштабирующая матрица  для i -го радиального нейрона имеет диагональную форму, в которой только элементы
для i -го радиального нейрона имеет диагональную форму, в которой только элементы 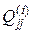 принимают ненулевые значения. В такой системе отсутствует круговое перемешивание сигналов, соответствующих различным компонентам вектора x, а элемент
принимают ненулевые значения. В такой системе отсутствует круговое перемешивание сигналов, соответствующих различным компонентам вектора x, а элемент 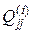 играет роль индивидуального масштабирующего коэффициента для j- го компонента вектора x i -го нейрона. На рис. 4.4 представлена детальная структура сети HRBF с произвольной матрицей
играет роль индивидуального масштабирующего коэффициента для j- го компонента вектора x i -го нейрона. На рис. 4.4 представлена детальная структура сети HRBF с произвольной матрицей 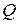 . В сетях HRBF роль коэффициентов
. В сетях HRBF роль коэффициентов 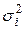 выполняют элементы матрицы Q, которые уточняются в процессе обучения.
выполняют элементы матрицы Q, которые уточняются в процессе обучения.
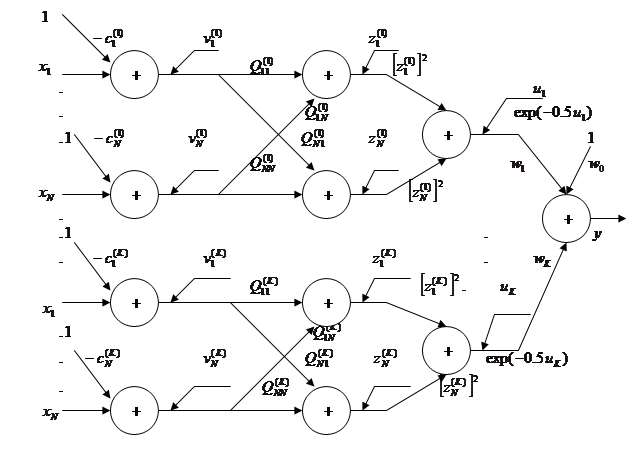 |
Рис. 4.4 Детальная структура радиальной сети HRBF с произвольной масшабирующей матрицей Q
 2014-02-02
2014-02-02 791
791








