ЧАСТЬ 2.
Закон Кирхгофа. Зависимость теплового эффекта химической реакции от температуры
Закон Гесса. Тепловые эффекты химических реакций
Тепловым эффектом называется количество выделенной или поглощенной теплоты при следующих условиях: система совершает только работу расширения, объем или давление остаются постоянными, температуры исходных и конечных веществ одинаковы, реакция протекает практически до конца.
Для расчета тепловых эффектов различных процессов, (в том числе и состоящих из нескольких этапов) в термодинамике применяют закона Гесса (установлен экспериментально Г.И. Гессом), который формулируется следующим образом: «Тепловой эффект химической реакции не зависит от пути процесса, а определяется лишь состоянием исходных и конечных веществ, в ней участвующих». Тепловой эффект химической реакции равен разности сумм произведений энтальпий образования конечных и исходных веществ на стехиометрические коэффициенты в уравнении реакции.
DrH0298=ånкон(DfH0298)кон-ånнач(DfH0298)нач
Для различных веществ при нормальных условиях (Р0=101,3 кПа; Т0=298К) энтальпии образования обозначаются как DfН0298, кДж/моль и приводятся справочниках физико-химических величин.
Для реальных систем закон Гесса используют при вычислении общего количества теплоты, необходимого для нагревания (или выделяющегося при охлаждении) любой системы от Т1 до Т2 при Р=соnst, где Т1 ³Т0:
Qp=nòсp(T)dT
Qp=DH=n[a(T-T0)+b/2(T2-T20)+c/3(T3-T30)+c/(1/T0-1/T)+d/4(T4-T40)].
Тепловой эффект процесса зависит от температуры. Эта зависимость определяется законом Кирхгофа, который формулируется следующим образом: «Частная производная от теплового эффекта по температуре равна разности теплоемкости системы в конечном и исходном состояниях». Для процессов, протекающих при постоянном давлении, этот закон выражается уравнением:
dQp/dT=d(DrH)/dT=å(nCp)кон-å(nCp)исх=DrCp
Закон Кирхгофа справедлив для любых процессов при условии, что W/=0, т.е. W=Wрасш. Для приближенных расчетов: Qp=DrH0298+Dra(T-298)-(T2-2982)Drb/2. Где: Dra=å(na)кон-å(na)исх.; Drb=å(nb)кон.-å(nb)исх..
Задачей второго закона термодинамики является определение условий, в которых возможно протекание самопроизвольных процессов, и условий, при которых наступает равновесие.
Коэффициент полезного действия (кпд) тепловой машины, работающей по квазистатическому циклу Карно, не зависит от природы рабочего тела, а определяется только интервалом температур, в котором совершается работа. Справедливость этой посылки в термодинамике доказывает теорема Карно-Клаузиуса, являющаяся одной из формулировок II закона термодинамики:
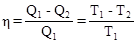 , где: Q1 – теплота, сообщенная рабочему телу при температуре Т1 от источника тепла; Q1 – теплота, отданная телом при температуре Т2 холодильнику.
, где: Q1 – теплота, сообщенная рабочему телу при температуре Т1 от источника тепла; Q1 – теплота, отданная телом при температуре Т2 холодильнику.
Основной формулировкой второго закона является формулировка Больцмана: «Все процессы в природе переводят систему из состояния менее вероятного в более вероятное».
В 1865 г. Клаузиус ввел новую функцию состояния S – энтропию, являющуюся мерой хаоса, неупорядоченности системы, которая принята в качестве меры вероятности: 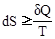 (математическая запись второго начала).
(математическая запись второго начала).
Второе начало имеет статистическую интерпретацию: S=k*ln(w) (формула Больцмана), где: k=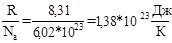 – константа Больцмана, w – термодинамическая вероятность (или статистический вес) макросостояния.
– константа Больцмана, w – термодинамическая вероятность (или статистический вес) макросостояния.
Величина, равная dQ/T, называется приведенным теплом и является рассеянной теплотой, следовательно и энтропия характеризует рассеянность теплоты; размерность ее соответствует [Дж/моль×К]. В изолированной системе (Q=0) приращение энтропии при равновесии равно приведенному теплу, а в самопроизвольных процессах больше приведенной теплоты. Энтропия является функцией состояния системы и однозначно определяется ее параметрами.
 2014-02-02
2014-02-02 4790
4790
