2014-02-02
615
Рис. 5.26
Рис. 5.25
Рис. 5.24
Рис. 5.23
Рис. 5.22
На систему действуют случайные возмущения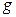 
и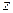 
с известными спектральными плотностям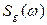и 
и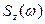 
. Задающее воздействие 
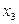также является случайным сигналом со спектральной плотностью 
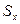. Пусть все три воздействия – центрированные сигналы. Тогда и сигнал ошибки 
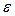тоже будет центрированным.
Если внешние воздействия не коррелированны между собой, то сигнал ошибки 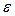, возникающий в системе, может рассматриваться как сумма трех независимых составляющих:
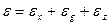(5.58)
Составляющая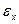 
обусловлена неточным воспроизведением задающего воздействия, а составляющие 
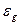и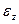 
- неполным подавлением возмущени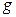й и 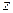. Соответственно дисперсия сигнала ошибки будет определяться как:
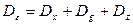(5.59)
Дисперсия случайного сигнала согласно (5.57) зависит от амплитудной частотной характеристики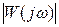 
, которая определяется на основе передаточной функции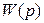 
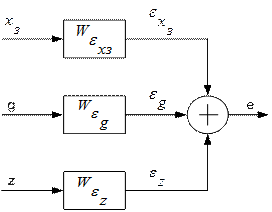
Передаточные функци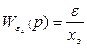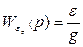и 
, 
и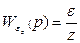 
могут быть вычислены по схемам:
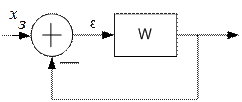
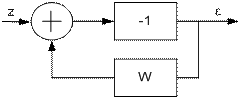
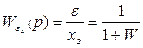(5.60)
(5.61)
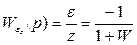(5.62)
Каждая из дисперсий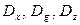 
определяется по формулам:
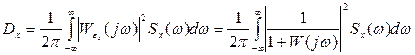(5.63)
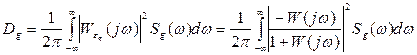(5.64)
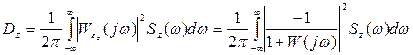(5.65)
При подстановке в формулы (5.63)-(5.65) конкретных значени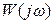й 
и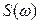 
получаются довольно сложные выражения, интегрирование которых обычными методами затруднительно. Поэтому используют следующий прием. Подынтегральное выражение представляют в типовой форме – в виде отношения двух полиномов от переменной 
:
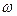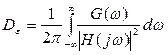, (5.66)
где
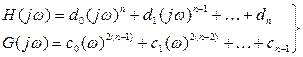(5.67)
Полином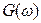 
всегда имеет степень ниже 
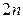и содержит только четные степени 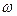. Если в числителе окажутся нечетные степени, их можно отбросить.
В полиноме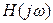 
в виде сомножителя входит характеристическое уравнение замкнутой системы. Поэтому при приближении системы к границе устойчивости интеграл (5.66) резко возрастает.
Интегралы вида (5.66) для различных степеней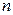 
вычислены заранее и приведены в справочниках по теории управления. Для степеней 
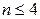интегралы равны:
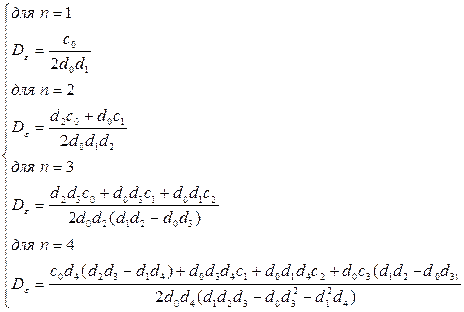(5.68)
Представление интегралов (5.63)- (5.65) в форме (5.66) возможны практически для любой реальной системы, не содержащей запаздывание. Получив таким образом аналитическое значение дисперсии ошибки, получаем функцию от параметров системы:
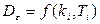, (5.69)
где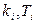 
- параметры системы. Минимизируя выражение (5.69) по параметрам 
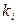и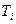 
, можно определить их оптимальные значения.
Пример
Определить оптимальное значение передаточного коэффициента с передаточной функцией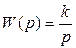 
.
На входе системы действует задающее воздействие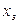 
со спектральной плотностью 
.
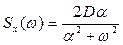На систему действует возмущение 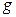в виде белого шума с ограниченной спектральной плотностью 
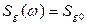для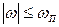 
.
Внешнее воздействие 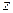отсутствует.
Таким образом, дисперсия сигнала ошибки определяется:
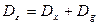
Дисперсия, обусловленная неточным воспроизведением задающего воздействия, имеет вид:
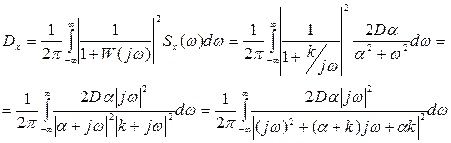
Сравнивая выражение с типовой формой записи интеграла (66), можно получить:
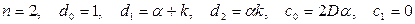
Окончательно дисперсия имеет вид:
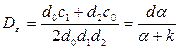
нетрудно заметить, что чем больше коэффициент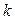 
, тем меньше дисперсия 
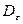, то есть тем точнее система воспроизводит на выходе задающее воздействие.
Дисперсия, обусловленная неполной компенсацией возмущения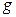
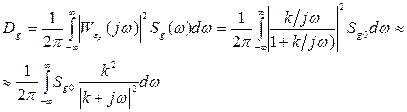
У этого интеграла:
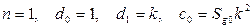
Окончательно дисперсия имеет вид:
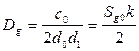
Чем больше коэффициент 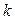, тем больше ошибка из-за прохождения возмущения 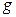на выход системы.
Суммарная дисперсия сигнала ошибки:
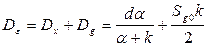
Оптимальное значение коэффициента усиления 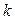найдем из условия:
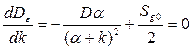
Откуда имеем:
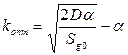
оптимальное значение передаточного коэффициента системы зависит от соотношения уровней задающего и возмущающего воздействий.
