2014-02-02
416
Рис. 5.18.
Наиболее просто определяется связь между математическими ожиданиями этих сигналов. Так как у стационарных сигналов математические ожидания являются постоянными величинами, то связь между ними определяется уравнением статики звена:
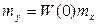(5.43)
Преобразование входного сигнала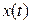 
в выходной сигнал 
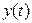можно рассматривать во временной и частотной областях.
Выходной сигнал 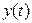связан с входным сигналом :
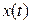, (5.44)
где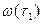 
- импульсная переходная характеристика звена, 
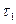- переменная интегрирования.
Определим взаимнокорреляционную функцию сигналов 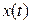и :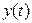
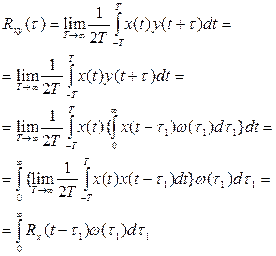(5.45)
Таким образом, взаимнокорреляционная функция сигналов 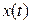и 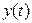определяется по формуле:
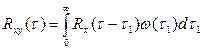(5.46)
Так как интеграл (5.46) имеет такой же вид, как и (5.44), то функцию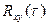 
можно рассматривать как реакцию линейной системы на воздействие, имеющее форму корреляционной функции 
.
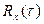Определи корреляционную функцию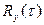 
:
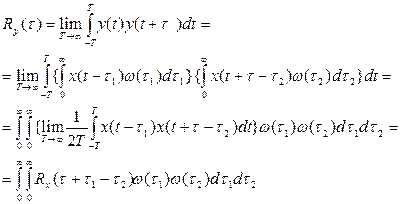(5.47)
Таким образом, корреляционная функция выходного сигнала 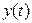определяется по формуле:
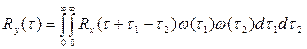(5.48)
Выражение (5.48) показывает, что корреляционная функция выходного сигнала может быть получена двукратным взятием интеграла свертки от корреляционной функции 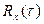входного сигнала.
Таким образом, преобразование линейной системы случайного входного сигнала в случайный выходной сигнал связано с корреляционными взаимнокорреляционной функциями и представлено.Рис. 5.19.
