Группировка значений факторного и результативного признаков Таблица 4
....
.....
.. …. …. ….
.. ….. ….. …
... …... …..
|
|
|
Однако большое число единиц в совокупности, а также, если одному значению факторного признака соответствует несколько значений результативного признака, затрудняет восприятие рядов.
В таких случаях целесообразнее воспользоваться для установления факта наличия связи корреляционными таблицами.
4) Построение корреляционной таблицы начинают с группировки значений факторного и результативного признаков. Так как в приводимом примере факторный признак представлен всего пятью вариантами повторяющихся значений, достаточно в первом столбце табл. 4 записать эти варианты.
Для результативного признака необходимо определить величину интервала. Для этого воспользуемся формулой Стерджесса:
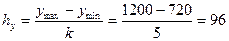 человек,
человек,
где k=1+3,322*lg20=5
В корреляционной таблице факторный признак, как правило, располагают в строках, а результативный признак у — в столбцах (графах) таблицы. Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту повторения данного сочетания значений х и у (табл. 2).
| Центральное значение интервала | fx | 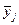 | х*fx | x2*fx | |||||
| Группы по у Группы по х | 720-816 | 817-913 | 914-1010 | 1011-1107 | 1108-1204 | ||||
 8 8 | - | - | |||||||
| - | |||||||||
| - | |||||||||
| - | |||||||||
| - | - | ||||||||
| fy | - | ||||||||
| yfy | - | - | - | ||||||
| xyfy | - | - | - |
Примечание. yj—среднее значение результативного признака j-й группы значений факторного признака; xyfxy=768*8*2 + 768*9*1=19200 (см. табл.)
fx — частота повторения данного варианта значения факторного признака для всей совокупности;
 fy —частота повторения результативного признака по всей совокупности.
fy —частота повторения результативного признака по всей совокупности.
По данной корреляционной таблице можно сделать предположение о наличии или отсутствии связи, а также выяснить ее направление. Если частоты в корреляционной таблице расположены по диагонали из левого верхнего угла в правый нижний угол (т.е. большим значениям фактора соответствуют большие значения функции), то можно предположить наличие прямой корреляционной зависимости между признаками. Если же частоты расположены по диагонали справа налево (из правого верхнего угла в левый нижний угол), то предполагают наличие обратной связи между признаками.
О тесноте связи между признаками x и y можно судить по кучности расположения частот вокруг диагонали. Если клетки заполнены большими цифрами, то связь слабая. Чем ближе частоты (fxy) располагаются к одной из диагоналей, тем теснее связь. Если в расположении частот (fxy) нет системности, то можно судить об отсутствии связи.
Для более четкого выявления основной тенденции связи, можно для каждой строки рассчитать средние значения результативного признака, соответствующие значению признака-фактора.
Корреляционная таблица позволяет компактно изложить материал, поэтому все последующие расчеты (показателей тесноты связи и параметров уравнения регрессии) можно вести по корреляционной таблице, что особенно удобно при значительном объеме исходных данных.
При корреляционной зависимости изменяются средние значения результативного признака в зависимости от того, какие значения принимает факторная переменная. Но поскольку на результативный признак влияет несколько факторов, то проявление закономерности затемняется влиянием случайностей. При вычислении средних значений результативного признака мы частично пренебрегаем влиянием случайных факторов. При вычислении параметров теоретической линии связи, мы получаем однозначное изменение переменной у с изменением фактора х.
Теоретической линией регрессии называется линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи. Теоретическая линия регрессии линия должна быть проведена так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии регрессии равнялась нулю, а сумма квадратов этих отклонений была бы минимальной величиной.
Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками.
Необходимо провести содержательный анализ природы изучаемой зависимости и сделать выводы относительно направления связи, возможности его изменения в исследуемой совокупности.
Приблизительное представление о линии связи можно получить, используя графический метод.
Можно также использовать опыт предыдущих исследований, и там, где выбранные формы уравнений связи давали удовлетворительный результат, рекомендовать их использовать в дальнейшем.
Наиболее часто для характеристики связей экономических показателей используют следующие типы функций:
 |
В нашем примере (зависимости числа туристов от затрат фирмы на рекламу) эмпирическая линия регрессии все же больше всего приближается к прямой и, следовательно, теоретическая линия регрессии может быть представлена уравнением вида:
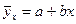 (Данная запись читается как «игрек выровненный по x»)
(Данная запись читается как «игрек выровненный по x»)
Для нахождения параметров а и b уравнения регрессии используем метод наименьших квадратов. При применении метода наименьших квадратов, считается, что сумма квадратов отклонений эмпирических точек теоретической линии регрессии должна быть величиной минимальной:
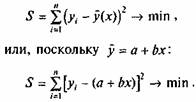 |
Следовательно, применение метода наименьших квадратов для определения параметров а и bпрямой, наиболее соответствующей эмпирическим данным, сводится к задаче на экстремум.
Функция двух переменных S(а, b) может достигнуть экстремума в том случае, когда первые частные производные этой функции равняются нулю, т.е. когда:
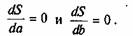 |
Вычисляя эти частные производные, получим
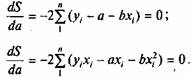 |
После несложных преобразований получим систему нормальных уравнений способа наименьших квадратов для определения величины параметров а и b уравнения прямолинейной корреляционной связи по эмпирическим данным:
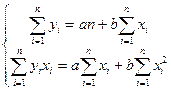 (2) (2) |
Решая систему уравнений (2) относительно a и b, получим следующие формулы для определения этих параметров:
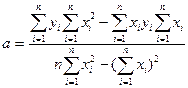 =(19050*2013-192310*199)/20*2013-1992=77960/659=118,3
=(19050*2013-192310*199)/20*2013-1992=77960/659=118,3
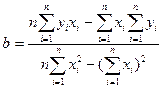 =20*192310-199*19050/659=55250/659=83,84
=20*192310-199*19050/659=55250/659=83,84
Для определения коэффициентов a и b составим вспомогательную таблицу 5
Получим систему уравнений
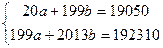
Таблица 5
| № п/п | Затраты на рекламу (усл. ден. ед.) х | Кол-во туристов, воспользовавшихся услугами фирмы, чел. У | x*y | x^2 | y регрессии | y регрессии по корреляционной таблице | у2 |
| Итого 20 | 19050,16 | 18754,97 |
В результате: а = 118,3; b= 83,84 и 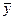 = 118,3+ 83,84x.
= 118,3+ 83,84x.
Параметр a – это свободный член уравнений регрессии, он определяет положение начальной точки линии регрессии в системе координат при х=0 y=а
Параметр b называется коэффициентом регрессии, является угловым коэффициентом линии регрессии и показывает, насколько изменяется в абсолютном значении результативный признак при изменении на единицу признака фактора х.
Если данные сгруппированы (например, представлены в виде корреляционной таблицы 4), то система нормальных уравнений имеет вид
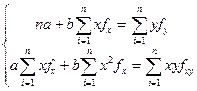 |
где fx— частота повторения данного варианта значения у;
fy — частота повторения данного варианта значения х;
fxy — частота повторения данного сочетания значений х и у
Для нашего примера имеем:
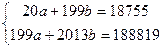
Выражаем из первого уравнения системы показатель a, подставляем во второе уравнение системы
а=937,75-9,95b; 937,75-9,95b +10,12b=948,84; b=11,09/0,166=66,81;
а=937,75-9,95*66,81=273,02 и получаем
a=273,02; b=66,81
Уравнение регрессии будет иметь вид: 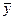 = 273,02 + 66,81x
= 273,02 + 66,81x
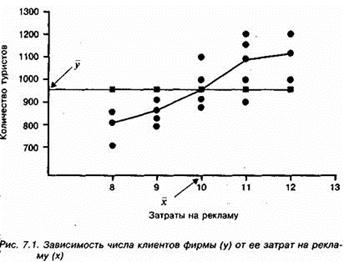
Графическое изображение эмпирической и теоретической линии связи представлено на рис. 1.
 |
Для нахождения параметров гиперболы 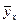 =а+b/х по способу наименьших квадратов пользуются аналогичной прямолинейной зависимости системой нормальных уравнений, в которой х заменен на 1/х.
=а+b/х по способу наименьших квадратов пользуются аналогичной прямолинейной зависимости системой нормальных уравнений, в которой х заменен на 1/х.
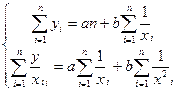
Для определения параметров параболы второго порядка 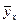 =а+bх+сх2 в соответствии метода наименьших квадратов решается система, состоящая из трех нормальных уравнений:
=а+bх+сх2 в соответствии метода наименьших квадратов решается система, состоящая из трех нормальных уравнений:
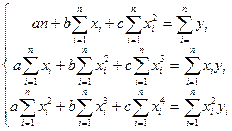
Выбор теоретической формы корреляционной связи всегда несколько условен, так как в действительности зависимости между признаками лишь приблизительно соответствуют функциональным. Поэтому только при высокой тесноте связи между признаками линия регрессии имеет содержательный смысл и практическое значение.
 2014-02-02
2014-02-02 1365
1365
