Корреляционно-регрессионный анализ

Количественные критерии оценки тесноты связи Таблица 1

Порядок изучения статистической связи. Классификация связей в статистике.

Важная задача статистики состоит в выявлении существующих связей между явлениями. Социально-экономические явления представляют собой результат одновременного воздействия большого числа факторов. При изучении эти явлений необходимо выявить основные факторы и абстрагироваться (не принимать во внимание) от второстепенных.

Рассматривая зависимости между признаками, выделяют две категории связи функциональную и стохастическую.

Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Например, функциональной является зависимость длины окружности или площади круга от радиуса. Модель функциональной связи может быть представлена как Y=f(X). На практике такие связи встречаются в математических формула, а также при расчете сдельной оплаты труда, (если принять за у оплату труда, а за х кол-во изготовленных изделий и учесть, что за каждое изделие оплата 5 руб, то тогда оплата труда выражается зависимостью y=5*x. Такие зависимости называются жестко детерминированными.

В действительности же взаимосвязи в социально-экономических явлениях значительно сложнее, они многофакторные и не носят функционального характера. Поэтому статистикой изучаются стохастические связи. Стохастическая связь- это такая связь между признаками, при которой для каждого значения признака фактора Х признак-результат Y может в определенных пределах принимать любые значения с некоторыми вероятностями, при этом его статистические характеристики (например, среднее значение) изменяется по определенному закону.

Модель стохастической связи может быть представлена в общем виде уравнение Y=f(X, u), где Y-фактическое значение результативного признака;

f(X) –часть результативного признака, сформировавшегося под воздействием фактора X или нескольких факторов X₁, X₂ …X_n;

f(u) - случайная составляющая, часть результативного признака, которая возникла вследствие влияния прочих факторов, а также ошибок измерения признаков.

Частным случаем стохастической связи является корреляционная связь. Это такая связь, при которой с изменением значения признака X закономерно изменяется среднее значение признака Y, в то время как в каждом отдельном случае признак Y с определенной вероятностью может принимать множество различных значений.

Модель корреляционной связи: E(Y/X_1, X₂, … X_m)=f(X_1, X₂, … X_m), Где m – множество факторов, Е - математическое ожидание.

Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению и аналитическому выражению.

По степени тесноты связи различают количественные критерии оценки тесноты связи по шкале Чеддока.

Величина коэффициента	Характер связи
До ± 0,3	Практически отсутствует
± 0,3 - ± 0,5	Слабая
± 0,5 - ± 0,7	Умеренная
± 0,7 - ± 1,0	Сильная

Предварительная характеристика направления и тесноты связи между признаками может быть произведена с помощью непараметрических показателей связи: коэффициента Фехнера, коэффициентов корреляции рангов (Спирмена, Кендалла), коэффициента конкордации.

Коэффициент Фехнера Кф оценивает направление и тесноту связи на основе сравнения знаков отклонений значений результативного у и факторного х признаков от их средних арифметических: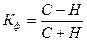

где С — число совпадений знаков отклонений у от 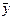и х от 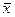по всем единицам изучаемой совокупности; Н — число случаев несовпадений знаков отклонений.

Рассчитаем коэффициент Фехнера для рассматриваемого примера. Сравним уровни заработной платы и производительности труда по всем работникам с их средними значениями: 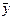= 41280/24 = 1720 руб./чел., 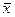= 69600/24 = = 2900 руб./чел. Подсчитаем совпадение знаков отклонений по обоим признакам (табл. 2).

Взаимосвязь уровней производительности труда и заработной платы почтовых работников и расчетные величины для оценки тесноты связи между ними Таблица 2

Номер работ-ника	Производит. труда х, руб. чел.	Заработная плата у, руб.чел.	Знак отклонения от среднего уровня	Совпадения (несовпадение) знаков	Ранги	Разность рангов d	d2
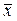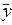		Rx	Ry
			-	-	C			-1
			-	-	C
			-	-	C
			-	-	C			-1
			-	-	C			-4
			-	-	C
			-	-	C
			-	-	C	8,5		2,5	6,25
			-	-	C	8,5		0,5	0,25
			-	-	C
			-	-	C
			-	+	Н
			+	-	Н
			+	+	С
			+	+	С			-1
			+	-	Н	16,5		3,5	12,25
			+	+	С	16,5		-0,5	0,25
			+	+	С
			+	+	С	19,5		4,5	20,25
			+	+	С	19,5		-0,5	0,25
			+	+	С
			+	+	С			-1
			+	+	С
			+	+	С
Итого			-	-	-	-	-	-	95,5

Коэффициент Фехнера для нашего примера равен 0,75[(21-3)/24]. Это дает основание считать, что между производительностью труда работников почтовой связи и их заработной платой существует достаточно тесная прямая связь.

Коэффициент корреляции рангов 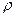(коэффициент Спирмена) учитывает согласованность рангов, т.е. номеров или мест, которые занимают единицы совокупности по каждому из анализируемых признаков, и рассчитывается по формуле:

,

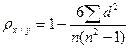где п — количество единиц совокупности; d — разность рангов по признакам х и у.

Порядок сопоставления рангов факторного и результативного показателей таков: единицы совокупности ранжируются по факторному и результативному признакам и каждой единице присваивается номер (место) в упорядоченном ряду признаков. Если встречаются в ряду одинаковые варианты по результативному и факторному признакам, то каждой из них присваивается среднее арифметическое значение их рангов. Коэффициент корреляции рангов может принимать значения от —1 до+1.

В рассматриваемом примере работники почтовой связи ранжированы по возрастанию факторного признака — уровню производительности труда с 1-го по 24-й номер. При ранжировании почтовых работников трижды встретились одинаковые варианты: х = 2550 у работников, занимающих 8-е и 9-е места, х = 3170 у работников, занимающих 16-е и 17-е места, и х = 3600 у работников, занимающих 19-е и 20-е места по возрастанию производительности труда, поэтому им присвоены средние ранги: 8,5; 16,5 и 19,5.

Коэффициент корреляции рангов составил 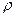=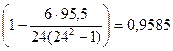, что подтверждает ранее полученный вывод о положительной тесной связи между признаками.

Достоинством непараметрических показателей связи является возможность их использования при анализе взаимосвязи социально-экономических явлений, не имеющих количественного выражения (атрибутивных признаков, например, зависимости заработной платы от уровня образования; от формы собственности предприятия - государственной, частной, кооперативной.

Для определения тесноты связи между произвольным числом признаков применяют множественный коэффициент ранговой корреляции (коэффициент конкордации):

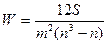, где

m- количество факторов; n-число наблюдений; S-отклонения суммы квадратов суммы рангов по всем факторам от среднего квадрата суммы рангов.

Например, Произведем оценку взаимосвязи между уставным капиталом, количеством и ценой выставляемых на аукцион акций связи. Данные приведены в таблице.

Номер организации	Уставной капитал, х млн. руб.	Число акций у, ед.	Цена акции z, тыс. руб.	Rx	Ry	Rz	Сумма рангов	Квадрат суммы рангов
	310,6		2,3
	245,0		2,1
	147,6		1,9
	185,3		1,8
	420,2		2,5
	570,1		2,6
	263,2		2,4
	80,8		2,2
	127,3		1,6
	346,2		2,0
Итого	-	-	-	-	-	-

S=3333-(165²/10)=3333-2722,5=610,5 W=

Величина коэффициента конкордации W свидетельствует о весьма тесной связи между размером организации, числом выставляемых акций и их ценой.

Для оценки тесноты связи между двумя признаками исчисляется эмпирическое корреляционное отношени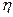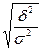е =, где 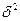-межгрупповая дисперсия; 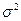-общая дисперсия.

²-коэффициент детерминации.

Если коэффициент детерминации >0,7, то связь между признаками достаточно тесная.

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются в противоположном направлении по сравнению с изменением факторного.

По аналитическому выражению выделяют связи прямолинейные (связь между явлениями приближенно выражена уравнением прямой линии) и нелинейные (криволинейные) (связь выражена уравнением кривой линии: гиперболы, параболы и др.)

Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила связи и ее направление, а в регрессионном исследуется ее форма.

Простейшим приемом обнаружения связи является:

1) сопоставление двух параллельных рядов — ряда значений факторного признака и соответствующих ему значений результативного признака. Значения факторного признака располагают в возрастающем порядке и затем прослеживают направление изменения величины результативного признака. Результативный признак (функцию) в дальнейшем будем обозначать через у, а факторный признак — через х.

В тех случаях, когда с возрастанием факторного признака возрастает величина результативного признака, то можно говорить о наличии прямой корреляционной связи. Если же с увеличением факторного признака величина результативного признака уменьшается, то можно предполагать обратную связь между признаками.

x
y

Мы видим, что с увеличением величины х величина у также растет. Значит связь между признаками – прямая.

2) Метод группировок. Проводится группировка единиц совокупности по факторному признаку. Для каждой группы рассчитывается среднее значение результативного признака. Если факторный признак и среднее значение результативного признака изменяется в одном направлении, то связь прямая, если в разных – обратная, если нет закономерности, то связь отсутствует.

Затраты на рекламу (усл. ден. ед.)
Среднее число туристов, воспользовавшихся услугами фирмы, чел.				1062,5

3) Статистическую связь между двумя признаками можно изобразить графически и по графику судить о наличие, о направлении и форме связи. При этом на оси абсцисс откладывают значение факторного признака, а по оси ординат – результативного.

. … …. …..