Задача принятия решения, рассматриваемая в рамках системного подхода, содержит три основные компоненты: в ней выделены система, управляющая подсистема и среда. Теперь мы переходим к изучению задач принятия решения, в которых на систему воздействует не одна, а несколько управляющих подсистем, каждая из которых имеет свои цели и возможности действий. Такой подход к принятию решений называется теоретико-игровым, а математические модели соответствующих взаимодействий называются играми. Ввиду различия целей управляющих подсистем, а также определенных ограничений на возможности обмена информацией между ними, указанные взаимодействия носят конфликтный характер. Поэтому всякая игра представляет собой математическую модель конфликта. Ограничимся случаем, когда управляющих подсистем две. Если цели систем противоположны, конфликт называется антагонистическим, а математическая модель такого конфликта называется антагонистической игрой..
В теоретико-игровой терминологии 1-я управляющая подсистема называется игроком 1, 2-я управляющая подсистема - игроком 2, множества
их альтернативных действий называются множествами стратегий этих игроков. Пусть Х - множество стратегий игрока 1, Y - множество стратегий
игрока 2. Состояние системы однозначно определяется выбором управляющих воздействий подсистемами 1 и 2, то есть выбором стратегий
x ∈ X и y ∈ Y. Пусть F (x, y)- оценка полезности для игрока 1 того состояния
системы, в которое она переходит при выборе игроком 1 стратегии х и
игроком 2 стратегии у. Число F (x, y) называется выигрышем игрока 1 в ситуации (x, y), а функция F - функцией выигрыша игрока 1. Выигрыш игрока
1 одновременно является проигрышем игрока 2, то есть величиной, которую первый игрок стремится увеличить, а второй – уменьшить. Это и есть
проявление антагонистического характера конфликта: интересы игроков полностью противоположны (то, что выигрывает один, проигрывает другой).
Антагонистическую игру естественно задать системой Г= (Х, Y, F).
Заметим, что формально антагонистическая игра задается фактически так же, как и задача принятия решения в условиях неопределенности - если
отождествить управляющую подсистему 2 со средой. Содержательное различие между управляющей подсистемой и средой состоит в том, что
поведение первой носит целенаправленный характер. Если при составлении математической модели реального конфликта у нас есть основание (или намерение) рассматривать среду как противника, цель которого - принести
нам максимальный вред, то такую ситуацию можно представить в виде антагонистической игры. Другими словами, антагонистическую игру можно трактовать как крайний случай ЗПР в условиях неопределенности,
характеризуемый тем, что среда рассматривается как противник, имеющий цель. При этом мы должны ограничить виды гипотез о поведении среды.
Наиболее обоснованной здесь является гипотеза крайней осторожности, когда, принимая решение, мы рассчитываем на самый худший для нас возможный вариант действий среды.
Определение. Если Х и Y конечны, то антагонистическая игра называется матричной. В матричной игре можно считать, что X ={1,…, n },
Y ={1,…, m } и положить aij=F (i,j). Таким образом, матричная игра полностью определяется матрицей A= (aij), i =1,…, n, j =1,…, m.
Пример 3.1. Игра с двумя пальцами.
Два человека одновременно показывают один или два пальца и называют число 1 или 2, означающее, по мнению говорящего, количество
пальцев, показанное другим. После того, как пальцы показаны и числа названы, происходит распределение выигрыша по следующим правилам:
если оба угадали или оба не угадали, сколько пальцев показал их соперник, выигрыш каждого равен нулю; если угадал только один, то противник платит угадавшему сумму денег, пропорциональную общему числу показанных
пальцев.
Это антагонистическая матричная игра. Каждый игрок имеет четыре стратегии: 1- показать 1 палец и назвать 1, 2- показать 1 палец и назвать 2, 3-
показать 2 пальца и назвать 1, 4 - показать 2 пальца и назвать 2. Тогда матрица выигрышей A=(aij), i= 1 ,…, 4, j= 1 ,…, 4 определяется следующим образом:
a12= 2, a21 = – 2, a13=a42= –3, a24=a31= 3, a34 = – 4, a43= 4 ,aij= 0 в остальных случаях.
Пример 3.2. Дискретная игра типа дуэли.
Задачами дуэльного типа описывается, например, борьба двух игроков,
каждый из которых желает совершить некое единовременное действие (выброс на рынок партии товара, заявка о покупке на аукционе) и выбирает для этого время. Пусть игроки продвигаются навстречу друг другу на n шагов. После каждого сделанного шага игрок может выстрелить или не выстрелить в противника. Выстрел может быть у каждого только один. Считается, что вероятность попасть в противника, если продвинуться на k
 шагов, равна
шагов, равна
k. Стратегия игрока 1(2) заключается в принятии решения
n
стрелять на i -м (j -м) шаге. Пусть i < j, 1-й игрок стреляет на i -м шаге, а игрок
2- на j -м шаге. Тогда выигрыш
aij
игрока 1 задается формулой
a = i
− (1 − i)
j = n (i −
j) + ij.



 ij n n n n 2
ij n n n n 2
Таким образом, выигрыш – это разность вероятностей поражения противника и собственного выживания в дуэли. В случае i > j первым стреляет
игрок 2 и
aij
= − aji. Если i = j, то полагаем
aij
= 0.
Игровая матрица,
умноженная для удобства на 5, при n =5 имеет вид
⎛ 0 − 3 − 7
⎜
⎜ 3 0 1
−11
− 2
−15 ⎞
⎟
− 5 ⎟
⎜ 7
⎜
|
⎝15
−1 0 7
2 − 7 0
5 − 5 15
5 ⎟.
⎟
|
0 ⎠
Матричным играм целиком посвящены 4-я и 5-я глава пособия.
Далее в тексте множества стратегий игроков Х и Y считаются ограниченными и замкнутыми, а функция F (x, y) - непрерывной.
Определение. Результатом, гарантированным игроку 1 при
использовании им стратегии х, называется число
min
y ∈ Y
F (x, y). Результатом,
гарантированным игроку 2 при использовании им стратегии у, называется
число
max
x ∈ X
F (x, y).
Определение. Нижней ценой игры Г= (Х, Y, F) называется величина
υ = max
 x ∈ X
x ∈ X
υ = min
min
y ∈ Y
max
F (x, y). Верхней ценой игры Г называется величина
F (x, y).
y ∈ Yx ∈ X
 Игрок 1 может гарантировать себе выигрыш, не меньший, чем υ, а
Игрок 1 может гарантировать себе выигрыш, не меньший, чем υ, а
 его противник может гарантировать себе проигрыш, не превышающий υ. В
его противник может гарантировать себе проигрыш, не превышающий υ. В
примере 3.1 υ = -2, υ=2. Следующая теорема поясняет происхождение
названий "нижняя цена игры" и "верхняя цена игры".
ТЕОРЕМА 3.1. Для любой непрерывной функции F (x, y), определенной на декартовом произведении компактов Х и Y, справедливо неравенство
 υ ≤υ, т.е.
υ ≤υ, т.е.
max
min
F (x, y) ≤
min
max
F (x, y). (3.1)
x ∈ X
y ∈ Y
y ∈ Y x ∈ X
Доказательство. Предварительно сформулируем следующую очевидную лемму:
ЛЕММА 3.1. Если Z - компактное множество, H (z) - непрерывная функция, то справедливы соотношения
∀ z ∈ Z
H (z) ≤ a ↔
max
z ∈ Z
H (z) ≤ a; (3.2)
∀ z ∈ Z
H (z) ≥ a ↔
min
z ∈ Z
H (z) ≥ a. (3.3)
Очевидно, что при всех х и у
min
y ′∈ Y
F (x, y ′) ≤ F (x, y) ≤
max
x ′∈ X
F (x ′, y).
Применив к этому неравенству лемму 3.1, получим требуемое соотношение (3.1).
Определение. Если в игре Г верхняя и нижняя цены совпадают, то
 говорят, что в этой игре выполнено соотношение минимакса. Число υ =υ=υ
говорят, что в этой игре выполнено соотношение минимакса. Число υ =υ=υ
называют ценой игры.
Определение. Пара стратегий (х 0, у 0) называется седловой точкой игры
Г, если выполняется соотношение
∀ x,y
F(x,y 0 ) ≤ F(x 0 ,y 0 ) ≤ F(x 0 ,y).
(3.4)
Смысл седловой точки состоит в том, что любой игрок, односторонне отступивший от нее, не выигрывает. Например, одностороннее отступление игрока 1 от седловой точки означает, что он выбрал не х 0, а другую стратегию x, в то время как 2-й по-прежнему придерживается стратегии у 0.
Если (i 0, j 0) - седловая точка в матричной игре, то элемент
минимальный в i0 -й строке и максимальный в j0 -м столбце матрицы.
a -
i 0 j 0
ТЕОРЕМА 3.2. В антагонистической игре Г= (Х, Y, F) седловая точка
(х 0, у 0) существует тогда и только тогда, когда выполнено соотношение минимакса
max
min
F (x, y) =
min
max
F (x, y). (3.5)
x ∈ X
y ∈ Y
y ∈ Y x ∈ X
При этом цена игры равна значению функции выигрыша в седловой точке, то
есть υ= F (x 0, y 0).
Доказательство.
Необходимость. Пусть (х 0, у 0) - седловая точка, то есть справедливо (3.4). С
учетом соотношений (3.2) и (3.3) это условие можно переписать в виде
max
x ∈ X
F (x, y 0) ≤ F (x 0, y 0) ≤
min
y ∈ Y
F (x 0, y). Но верны неравенства
min
max
F (x, y) ≤
max
F (x, y 0),
y ∈ Y x ∈ X
x ∈ X
min
y ∈ Y
F (x 0, y) ≤
max
x ∈ X
min
y ∈ Y
F (x, y).
Получаем неравенство
min
max
F (x, y) ≤
max
min
F (x, y),
которое вместе
y ∈ Yx ∈ X
с (3.1) дает требуемое равенство.
x ∈ X
y ∈ Y
Достаточность. Пусть справедливо (3.5). Выберем точки х 0 и у 0 так, чтобы они удовлетворяли условиям
min
y ∈ Y
max
F (x 0, y) =
F (x, y 0) =
max
x ∈ X
min
min
y ∈ Y
max
F (x, y),
F (x, y).
x ∈ X
Справедливы неравенства
min
y ∈ Y
y ∈ Yx ∈ X
F (x 0, y) ≤ F (x 0, y 0) ≤
max
x ∈ X
F (x, y 0).
Из способа выбора х 0 и у 0 вытекает, что
max
x ∈ X
F (x, y 0) = F (x 0, y 0) =
min
y ∈ Y
F (x 0, y).
Используя (3.2) и (3.3), получаем
(3.4), что и требовалось доказать.
Определение. Если (х 0, у 0) - седловая точка, то стратегия х 0 называется оптимальной для игрока 1, а стратегия у 0 – оптимальной для игрока 2. Непосредственный поиск седловых точек чаще всего проводится с помощью проверки истинности равенства (3.5).
Пример 3.3.
Игрок 1 выбирает число х из множества Х = [0; 1], игрок 2 выбирает число y из множества Y = [0; 1]. После этого игрок 2 платит игроку 1 сумму
F (x, y) = 2 x 2
− y 2.
Поскольку игрок 2 хочет минимизировать выигрыш игрока 1, то он
определяет
min(2 x 2 − y 2) = 2 х 2 −1,т.е. при этом y = 1. Игрок 1 желает
y ∈ Y
максимизировать свой выигрыш, и поэтому определяет
max(min F (x, y)) =
max(2 х 2 -1) = 2−1 = 1, который достигается при х =
x ∈ X
y ∈ Y
x ∈ X
1. Итак, нижняя цена игры равна
v = 1.
 Верхняя цена игры v =
Верхняя цена игры v =
min (max (2 х 2 − y 2)) =
min (2 − y 2) = 2−1 = 1, то
y ∈ Y
x ∈ X
y ∈ Y
 есть в этой игре v = v
есть в этой игре v = v
= 1. Поэтому цена игры v = 1, а седловая точка - (1;1).
Пример 3.4.
X = [0;1]; Y = [0;1]; F (x, y) = (x − y) 2.
 ψ(y)
ψ(y)
Найдем
ψ (y) =
ϕ (x) =
max
x ∈ X
min
y ∈ Y
F (x, y),
F (x, y).
0.25
2 (1- y) 2
Очевидно,
ϕ(x) = 0
(для любого x
y достигается при
y = x). На рис. 3.1.
|
|
0 0.5
ψ(y) = ⎪⎧
y 2, y ∈[0.5;1]
Рис. 3.1
(1− y)2, y ∈[0;0.5]
minψ(y)= (0.5)2 = 0.25. Этот минимум достигается в точке х =0.5, т.е.
y ∈ Y
в той точке отрезка [0;1], где значения функций y 2 и
(1− y)2
совпадают.
Получаем:
min
max
F (x, y) = 0.25;
max
min
F (x, y) = 0.
y ∈ Y x ∈ X
x ∈ X
y ∈ Y
нет.
Соотношение минимакса не выполнено, следовательно, седловой точки
Пример 3.5. Непрерывная дуэль.
Игроки движутся навстречу друг другу с постоянной скоростью. В
момент t =0 игроки достаточно далеко друг от друга, а при t =1 они сходятся
вплотную. На отрезке [0;1] задана вещественная функция
ai (t)- мера
меткости i -го игрока, i =1,2. Значение
ai (t)- вероятность того, что i -й игрок,
стреляя в момент t, поразит противника. Предполагается, что обе функции не
убывают, непрерывны и удовлетворяют краевым условиям
ai (0)= 0; ai (1)=1.
1-й игрок получает очки в количестве +1, если он поражает 2-го до того, как сам будет поражен; -1 в симметричном случае; и 0, если ни один не поражен, либо оба поражены одновременно.
Множества стратегий таковы: X = Y =[0;1]. Стратегия x игрока 1 означает:
«Я буду стрелять в момент t = x,если противник не выстрелит раньше. Если же он выстрелит, но промахнется, я для надежности буду стрелять в момент t =1». Аналогичны рассуждения второго. В качестве функции выигрыша берем математическое ожидание суммы, начисленной 1-му игроку, то есть
⎧2 a 1 (x)−1, x < y
F (x, y)= ⎪ a
(x)− a
(x), x = y
⎨ 1 2
|
(y), x > y.
Можно доказать, что множеством седловых точек 1-го игрока будет отрезок (возможно, и точка) I, определяемый из условия
I = { x 1 ∈ [0,1]|2 a 1 (x)−1=1− 2 a 2 (x)}.
Такой же отрезок (точка) составит
множество седловых точек 2-го игрока. Общее значение функций
2 a 1 −1 и
1− 2 a 2
на I будет ценой игры.
ТЕОРЕМА 3.3. В антагонистической игре все седловые точки эквивалентны, а оптимальные стратегии взаимозаменяемы, то есть если (х 1, у 1) и (х 2, у 2) - седловые точки, то (х 1, у 2) и (х 2, у 1) - также седловые точки, причем
F (x 1 ,y 1)= F (x 2 ,y 2)= F (x 1 ,y 2)= F (x 2 ,y 1). (3.6)
Доказательство. Поскольку (х 1, у 1) и (х 2, у 2) - седловые точки, то
справедливы соотношения
∀ x,y
∀ x,y
F(x,y 1 ) ≤ F(x 1 ,y 1 ) ≤ F(x 1 ,y).
F(x,y 2 ) ≤ F(x 2 ,y 2 ) ≤ F(x 2 ,y).
(3.7) (3.8)
Из них легко получить цепочки неравенств
F (x 2, y 2) ≤ F (x 2, y 1) ≤ F (x 1, y 1),
F (x 1, y 1) ≤ F (x 1, y 2) ≤ F (x 2, y 2),
которые влекут за собой систему равенств (3.6).
Для доказательства того, что (х 1, у 2) и (х 2, у 1) также седловые точки, нужно доказать выполнение cледующих условий:
∀ x, y
∀ x, y
F (x, y 2) ≤ F (x 1, y 2) ≤ F (x 1, y),
F (x, y 1) ≤ F (x 2, y 1) ≤ F (x 2, y).
Но эти условия с учетом (3.6) вытекают из (3.7) и (3.8).
ТЕОРЕМА 3.4. Если множества Х и Y ограничены, замкнуты и выпуклы, а функция F(x,y) непрерывна, вогнута по х при каждом фиксированном у и выпукла по у при каждом фиксированном х, то в антагонистической игре Г= (Х, Y, F) существует седловая точка.
Эту теорему примем без доказательства.
Игры с выпуклыми непрерывными функциями выигрыша называются выпуклыми. Это важный класс игр, рассмотрим некоторые его свойства.
ТЕОРЕМА 3.5.Пусть F (х, y) – непрерывная функция, заданная на единичном квадрате, строго выпуклая по y для любого х. Тогда имеется
единственная оптимальная стратегия y = y o∈[0;1] для игрока 2, значение y o
определяется как решение уравнения
max F (x,y o) =
x
v. Аналогично и для
игрока 1: если функция F (х,y) непрерывна по обоим аргументам и строго вогнута по х при любом y, то в этом случае игрок 1 имеет единственную оптимальную стратегию хо, определяемую из уравнения
min F (x 0, y) = v.
y
 Замечание. Если предполагать нестрогую выпуклость функции F (х,y) по y, то утверждения теоремы остаются в силе с той лишь разницей, что у игрока 2 оптимальная стратегия не будет единственной. Если предполагать нестрогую вогнутость функции F (х, y) по x, то утверждения теоремы остаются в силе с той лишь разницей, что у игрока 1 оптимальная стратегия не будет единственной.
Замечание. Если предполагать нестрогую выпуклость функции F (х,y) по y, то утверждения теоремы остаются в силе с той лишь разницей, что у игрока 2 оптимальная стратегия не будет единственной. Если предполагать нестрогую вогнутость функции F (х, y) по x, то утверждения теоремы остаются в силе с той лишь разницей, что у игрока 1 оптимальная стратегия не будет единственной.
Эту теорему также примем без доказательства.
Пример 3.6.


 ∂ 2 F
∂ 2 F
⎛π⎞2
π x y
 X = Y =[0;1]; F (х,y)=
X = Y =[0;1]; F (х,y)=
sin π(x + y). Так как
= −⎜
⎟ sin
(+) < 0

 2 ∂ x 2
2 ∂ x 2
⎝ 2 ⎠ 2
для x ∈[0; 1], y ∈(0;1), F (х,y) строго вогнута по х ∀ y ∈(0;1). Тогда цена игры
находится по формуле
v = max min sin π(x + y). При 0 ≤ х ≤ 1
 min
min
 x y 2
x y 2
2 0≤ y ≤1
 sinπ(x + y)
sinπ(x + y)
= sinπ
x, иначе
 min
min
sin π(x + y)
= sin π(x +1). Поэтому в
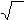 2 2 0≤ y ≤1 2 2
2 2 0≤ y ≤1 2 2
результате следующих вычислений получаем:
v = max { max
 min
min
sin π(x + y),
 max
max

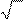

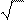
 min
min
sin π(x + y) } =
 0≤ x ≤1 0≤ y ≤1
0≤ x ≤1 0≤ y ≤1
2 1 ≤ x ≤1 0≤ y ≤1 2
 2
2
= max { max
sin π x,
max sin π(x +1) } = max {
2; 2 } = 2.

 0≤ x ≤1
0≤ x ≤1
2 1 ≤ x ≤1 2
2 2 2
Значение х, на котором достигается максимум, равно
1. Это же
 2
2
 значение будет решением уравнения
значение будет решением уравнения
 min
min
 0≤ y ≤1
0≤ y ≤1
sin π(x + y) =
2, т.к. минимум
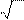 2
2
достигается при y = 0, и это уравнение превращается в следующее:

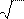
 sinπ x =
sinπ x =
2, откуда следует, что х = 1.
2 2 2
Заметим, что если в функции выигрыша поменять местами х и y, то
 она не изменится, следовательно, эта функция выпукла и по y при всех х
она не изменится, следовательно, эта функция выпукла и по y при всех х
∈[0;1]. Поэтому у игрока 2 существует оптимальная стратегия y o,
определяемая из уравнения

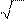
 maxsinπ(x + y) = 2.
maxsinπ(x + y) = 2.
0≤ x ≤1 2 2
Очевидно, максимум по х достигается при х =
1, и последнее

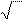

|
|
|
уравнение примет вид
sin ⎝2 ⎠ = 2.
2 2
Решением последнего уравнения будет y o= 0. Следовательно, игрок 2
имеет оптимальную стратегию y o= 0.
 2014-02-02
2014-02-02 2574
2574








