Общая схема применения метода ДП. Задача об оптимальном распределении ресурсов между отраслями на n лет
Рис. 4.8
Задача о распределении средств между предприятиями
Рассмотрим предложенную выше схему на конкретной задаче о распределении средств между предприятиями.
Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: 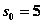 усл. ед. Размеры вложения в каждое предприятие кратны усл. ед. Средства x,выделенные k-мупредприятию (k=1, 2, 3, 4), приносят в конце года прибыль
усл. ед. Размеры вложения в каждое предприятие кратны усл. ед. Средства x,выделенные k-мупредприятию (k=1, 2, 3, 4), приносят в конце года прибыль 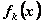 . Функции
. Функции 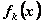 заданы таблично (табл. 4.1). Принято считать, что:
заданы таблично (табл. 4.1). Принято считать, что:
- прибыль 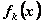 не зависит от вложения средств в другие предприятия;
не зависит от вложения средств в другие предприятия;
- прибыль от каждого предприятия выражается в одних условных единицах;
- суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.
Таблица 4.1
| x | 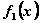 | 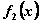 | 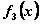 | 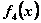 |
Решение. Обозначим через 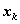 количество средств, выделенных k-мупредприятию. (Нумерацию предприятий 1, 2, 3, 4 сохраняем в процессе решения неизменной.)
количество средств, выделенных k-мупредприятию. (Нумерацию предприятий 1, 2, 3, 4 сохраняем в процессе решения неизменной.)
Суммарная прибыль равна
 | (4.18) |
Переменные xудовлетворяют ограничениям:
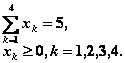 (4.19)
(4.19)
Требуется найти переменные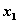 ,
, 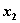 ,
, 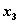 ,
, 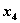 , удовлетворяющие системе ограничений (4.19) и обращающие в максимум функцию (4.18).
, удовлетворяющие системе ограничений (4.19) и обращающие в максимум функцию (4.18).
Особенности модели. Ограничения линейные, но переменные целочисленные, а функции 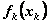 заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств 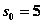 можно рассматривать как 4-шаговый, номер шага совпадет с номером предприятия; выбор переменных
можно рассматривать как 4-шаговый, номер шага совпадет с номером предприятия; выбор переменных 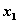 ,
, 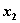 ,
, 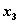 ,
, 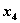 — управление соответственно на I, II, III, IV шагах.
— управление соответственно на I, II, III, IV шагах. 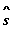 — конечное состояние процесса распределения — равно нулю, так как все средства должны быть вложены в производство,
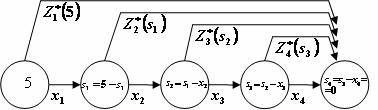
— конечное состояние процесса распределения — равно нулю, так как все средства должны быть вложены в производство, 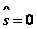 . Схема распределения показана на рис. 4.8.
. Схема распределения показана на рис. 4.8.
Уравнения состояний в данной задаче имеют вид:
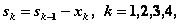 (4.20)
(4.20)
где 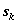 — параметр состояния — количество средств, оставшихся после k-го шага, т.е. средства, которые остается распределить между оставшимися 4-kпредприятиями.
— параметр состояния — количество средств, оставшихся после k-го шага, т.е. средства, которые остается распределить между оставшимися 4-kпредприятиями.
Введем в рассмотрение функцию 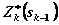 — условную оптимальную прибыль, полученную от k-го, (k+1)-го, …, 4-го предприятий, если между ними распределялись оптимальным образом средства
— условную оптимальную прибыль, полученную от k-го, (k+1)-го, …, 4-го предприятий, если между ними распределялись оптимальным образом средства 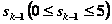 . Допустимые управления на k-мшаге удовлетворяют условию:
. Допустимые управления на k-мшаге удовлетворяют условию: 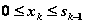 (либо k-мупредприятию ничего не выделяем,
(либо k-мупредприятию ничего не выделяем, 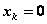 , либо не больше того, что имеем к k-мушагу,
, либо не больше того, что имеем к k-мушагу, 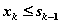 ).
).
Уравнения (4.13) и (4.16) имеют вид:
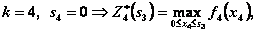 (а)
(а)
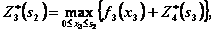 (б)
(б)
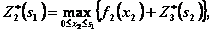 (в)
(в)
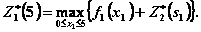 (г)
(г)
Последовательно решаем записанные уравнения, проводя условную оптимизацию (рис. 4.8) каждого шага.
IV шаг. В табл. 4.1 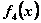 прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4-е предприятие. При этом для возможных значений
прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4-е предприятие. При этом для возможных значений 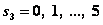 получим:
получим:
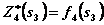 и
и 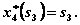
III шаг. Делаем все предположения относительно остатка средств 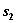 к III шагу (т.е. после выбора
к III шагу (т.е. после выбора 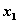 и
и 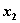 ).
). 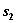 может принимать значения 0, 1, 2, 3, 4, 5 (например,
может принимать значения 0, 1, 2, 3, 4, 5 (например, 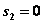 , если все средства отданы 1-му и 2-му предприятиям,
, если все средства отданы 1-му и 2-му предприятиям, 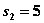 , если 1-е и 2-е предприятия ничего не получили, и т.д.). В зависимости от этого выбираем
, если 1-е и 2-е предприятия ничего не получили, и т.д.). В зависимости от этого выбираем 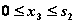 , находим
, находим 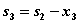 и сравниваем для разных
и сравниваем для разных 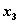 при фиксированном
при фиксированном 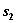 значения суммы
значения суммы 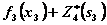 . Для каждого
. Для каждого 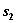 наибольшее из этих значений есть
наибольшее из этих значений есть 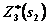 — условная оптимальная прибыль, полученная при оптимальном распределении средств
— условная оптимальная прибыль, полученная при оптимальном распределении средств 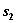 между 3-м и 4-м предприятиями. Оптимизация дана в табл. 4.2 при k =3. Для каждого значения
между 3-м и 4-м предприятиями. Оптимизация дана в табл. 4.2 при k =3. Для каждого значения 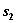
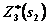 и
и 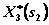 помешены в графах 5 и 6 соответственно.
помешены в графах 5 и 6 соответственно.
II шаг. Условная оптимизация, согласно уравнению (в), проведена в табл. 4.2 при k =2. Для всех возможных значений 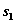 значения
значения 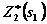 и
и 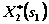 находятся в столбцах 8 и 9 соответственно; первые слагаемые в столбце 7 — значения
находятся в столбцах 8 и 9 соответственно; первые слагаемые в столбце 7 — значения 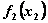 , взяты из табл. 4.1, а вторые слагаемые взяты из столбца 5 табл. 4.2 при
, взяты из табл. 4.1, а вторые слагаемые взяты из столбца 5 табл. 4.2 при 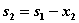 .
.
I шаг. Условная оптимизация (уравнение (г)) проведена в табл. 4.2 при k=1для 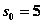 . Поясним решение подробно: если
. Поясним решение подробно: если  , то
, то 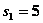 , прибыль, полученная от четырех предприятий при условии, что
, прибыль, полученная от четырех предприятий при условии, что 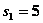 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна
ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна 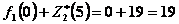 (
(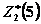 взято из столбца 9 табл. 4.2 при
взято из столбца 9 табл. 4.2 при 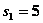 ). Если
). Если 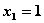 , то
, то  . Суммарная прибыль при условии, что
. Суммарная прибыль при условии, что  ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна
ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна 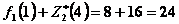 (
(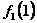 взято из табл. 4.1, a
взято из табл. 4.1, a 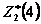 — из столбца 9 табл. 12.2.) Аналогично
— из столбца 9 табл. 12.2.) Аналогично
при 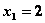 ,
, 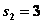 и
и 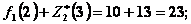
при 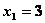 ,
, 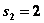 и
и 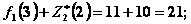
при 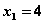 ,
, 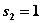 и
и 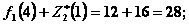
при 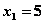 ,
, 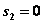 и
и 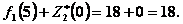
Сравнивая подчеркнутые числа, получим 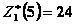 усл. ед. =
усл. ед. = 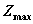 при
при 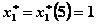 .
.
Используя уравнения (12.12), получим 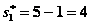 , а по табл. 4.2 в столбце 9 находим
, а по табл. 4.2 в столбце 9 находим 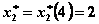 . Далее находим
. Далее находим 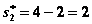 , а по табл. 4.2 в столбце 6 -
, а по табл. 4.2 в столбце 6 - 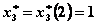 . Наконец,
. Наконец, 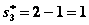 и
и 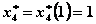 , т.е.
, т.е. 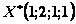 .
.
Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию — 2 усл. ед.; 3-му предприятию — 1 усл. ед.; 4-му предприятию — 1 усл.ед.►
Замечание 1. Решение четырехмерной задачи 4.9 на определение условного экстремума сведено фактически к решению четырех одномерных задач: на каждом шаге определялась одна переменная x.
Замечание 2. На разобранной задаче 4.9 видно, что метод ДП безразличен к виду и способу задания функции: 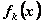 были заданы таблично, поэтому и
были заданы таблично, поэтому и 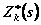 и
и 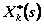 принимали дискретные значения, представленные в табл. 4.2.
принимали дискретные значения, представленные в табл. 4.2.
Таблица 4.2
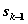 | 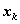 | 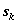 |  |  | 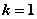 | ||||||
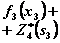 | 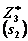 | 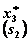 | 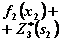 | 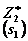 | 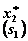 | 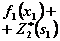 | 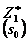 | 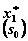 | |||
| 0+1=1 3+0=3 | 0+4=4 6+0=6 | 0+6=6 8+0=8 | |||||||||
| 0+6=6 3+4=7 4+0=4 | 0+7=7 6+4=10 9+0=9 | 0+10=10 8+6=14 10+0=10 | |||||||||
| 0+8=8 3+6=9 4+4=8 7+0=7 | 0+9=9 6+7=13 9+4=13 11+0=11 | 0+13=13 8+10=18 10+6=16 11+0=11 | |||||||||
| 0+13=13 3+8=11 4+6=10 7+4=11 11+0=11 | 0+13=13 6+9=15 9+7=16 11+4=15 13+0=13 | 0+16=16 8+13=21 10+10=20 11+6=17 12+0=12 | |||||||||
| 0+16=16 3+13=16 4+8=12 7+6=13 11+4=15 18+0=18 | 0+18=18 6+13=19 9+9=18 11+7=18 13+4=17 15+0=15 | 0+19=19 8+16=24 10+13=23 11+10=21 12+6=18 18+0=18 |
Замечание 3. Альтернативой между ДП для подобной дискретной задачи является метод перебора. Метод ДП предпочтительнее, так как на этапе условной оптимизации отбрасываются заведомо негодные варианты.
Замечание 4. Достоинством метода является возможность анализа решения на чувствительность к изменению 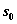 и n.
и n.
Замечание 5. К недостаткам метода по-прежнему следует отнести возникновение технических трудностей при вычислениях в случае увеличения размерности. Если каждое управление 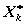 будет зависеть от r переменных, а состояние
будет зависеть от r переменных, а состояние 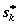 — от рпараметров, то на каждом шаге возникает rp-мерная задача оптимизации. (В задаче 12.1 r=1, p=1, т.е. решалась одномерная задача). Даже при реализации метода ДП на ЭВМ практически можно решать задачи для небольших r, p, n.
— от рпараметров, то на каждом шаге возникает rp-мерная задача оптимизации. (В задаче 12.1 r=1, p=1, т.е. решалась одномерная задача). Даже при реализации метода ДП на ЭВМ практически можно решать задачи для небольших r, p, n.
Прежде чем перейти к конкретным задачам, следует усвоить общую схему применения метода ДП.
Предположим, что все требования, предъявляемые к задаче методом ДП, выполнены. Построение модели ДП и применение метода ДП для решения сводится к следующим моментам:
1. Выбирают способ деления процесса управления на шаги.
2. Определяют параметры состояния 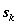 и переменные управления
и переменные управления 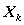 на каждом шаге.
на каждом шаге.
3. Записывают уравнения состояний.
4. Вводят целевые функции k-гошага и суммарную целевую функцию.
5. Вводят в рассмотрение условные максимумы (минимумы) 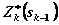 и условное оптимальное управление на k-м шаге:
и условное оптимальное управление на k-м шаге: 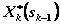 ,
, 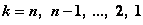 .
.
6. Записывают основные для вычислительной схемы ДП уравнения Беллмана для 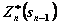 и
и 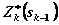 ,
, 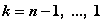 .
.
7. Решают последовательно уравнения Беллмана (условная оптимизация) и получают две последовательности функций:
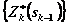 и
и 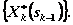
8. После выполнения условной оптимизации получают оптимальное решение для конкретного начального состояния 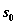 :
:
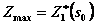 и
и
по цепочке 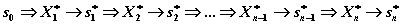 оптимальное управление:
оптимальное управление: 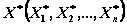 .
.
Решая задачи, следует по возможности придерживаться этой схемы по крайней мере в начале изучения темы. Рассмотрим, как работает схема на примере задачи об оптимальном распределении ресурсов между двумя отраслями на nлет.
Планируется деятельность двух отраслей производства на n лет. Начальные ресурсы 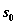 . Средства x, вложенные в I отрасль в начале года, дают в конце года прибыль
. Средства x, вложенные в I отрасль в начале года, дают в конце года прибыль 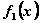 и возвращаются в размере
и возвращаются в размере 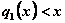 ; аналогично для II отрасли функция прибыли равна
; аналогично для II отрасли функция прибыли равна 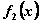 , а возврата —
, а возврата — 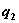
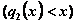 . В конце года все возвращенные средства заново перераспределяются между I и II отраслями, новые средства не поступают, прибыль в производство не вкладывается.
. В конце года все возвращенные средства заново перераспределяются между I и II отраслями, новые средства не поступают, прибыль в производство не вкладывается.
Требуется распределить имеющиеся средства 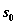 между двумя отраслями производства на n лет так, чтобы суммарная прибыль от обеих отраслей за nлет оказалась максимальной.
между двумя отраслями производства на n лет так, чтобы суммарная прибыль от обеих отраслей за nлет оказалась максимальной.
Необходимо: построить модель ДП для задачи и вычислительную схему; решить задачу при условии, что 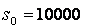 ед., n=4,
ед., n=4, 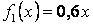 ,
, 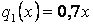 ,
, 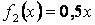 ,
, 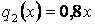 .
.
Решение.
Процесс распределения средств между двумя отраслями производства разворачивается во времени, решения принимаются в начале каждого года, следовательно, осуществляется деление на шаги: номер шага — номер года. Управляемая система — две отрасли производства, а управление состоит в выделении средств каждой отрасли в очередном году. Параметры состояния к началу k -го года — 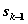 ( k=l, 2,..., n ) — количество средств, подлежащих распределению. Переменных управления на каждом шаге две:
( k=l, 2,..., n ) — количество средств, подлежащих распределению. Переменных управления на каждом шаге две: 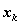 — количество средств, выделенных I отрасли, и
— количество средств, выделенных I отрасли, и 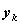 — II отрасли. Но так как все средства
— II отрасли. Но так как все средства 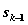 распределяются, то
распределяются, то  , и поэтому управление на k-мшаге зависит от одной переменной
, и поэтому управление на k-мшаге зависит от одной переменной 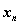 , т.е.
, т.е. 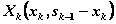 .
.
Уравнения состояний
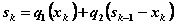 (4.21)
(4.21)
выражают остаток средств, возвращенных в конце k-гогода.
Показатель эффективности k-гошага — прибыль, полученная в конце k-гогода от обеих отраслей:
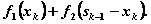 (4.22)
(4.22)
Суммарный показатель эффективности — целевая функция задачи — прибыль за nлет:
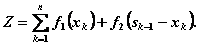 (4.23)
(4.23)
Пусть 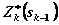 — условная оптимальная прибыль за n-k+1лет, начиная с k-гогода до n-гогода включительно, при условии, что имеющиеся на начало k-гогода средства
— условная оптимальная прибыль за n-k+1лет, начиная с k-гогода до n-гогода включительно, при условии, что имеющиеся на начало k-гогода средства 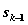 в дальнейшем распределялись оптимально. Тогда оптимальная прибыль за nлет
в дальнейшем распределялись оптимально. Тогда оптимальная прибыль за nлет 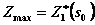 .
.
Уравнения Беллмана имеют вид:
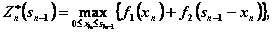 (4.24)
(4.24)
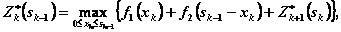 (4.25)
(4.25)
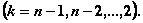
Используем конкретные данные.
Уравнение состояний (4.11) примет вид:
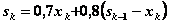 , или
, или 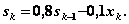 (4.26)
(4.26)
Целевая функция k-гошага (4.22)
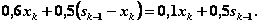
Целевая функция задачи
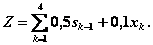 (4.27)
(4.27)
Функциональные уравнения
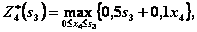 (4.28)
(4.28)
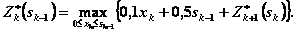 (4.29)
(4.29)
Проводим условную оптимизацию.
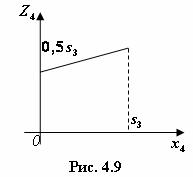
IV шаг. Используем уравнение (4.28). Обозначим через 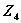 функцию, стоящую в скобках,
функцию, стоящую в скобках, 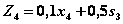 ; функция
; функция 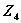 — линейная, возрастающая, так как угловой коэффициент 0,1 больше нуля. Поэтому максимум достигается на конце интервала
— линейная, возрастающая, так как угловой коэффициент 0,1 больше нуля. Поэтому максимум достигается на конце интервала 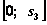 (рис. 4.9). Следовательно,
(рис. 4.9). Следовательно, 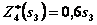 при
при 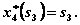
III шаг. Уравнение:
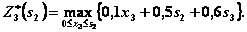
Найдем 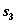 из уравнений состояний (4.26):
из уравнений состояний (4.26): 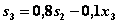 и, подставив его выражение в правую часть уравнения, получим
и, подставив его выражение в правую часть уравнения, получим
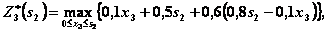
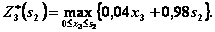
Как и в предыдущем случае, максимум достигается при 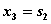 ; т.е.
; т.е.  при
при 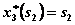 .
.
II шаг. Из уравнения состояния: 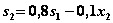 . Поэтому уравнение (4.28) при k =2 примет вид:
. Поэтому уравнение (4.28) при k =2 примет вид:
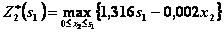 .
.
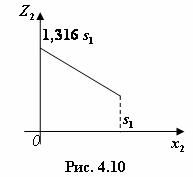
Линейная относительно 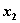 функция
функция 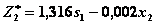 убывает на отрезке
убывает на отрезке 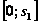 и поэтому ее максимум достигается при
и поэтому ее максимум достигается при 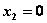 (рис. 4.10):
(рис. 4.10):
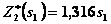 при
при 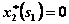 .
.
I шаг. 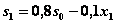 . Уравнение (4.28) при k=1имеет вид:
. Уравнение (4.28) при k=1имеет вид:
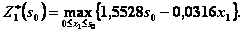
Как и в предыдущем случае, максимум достигается в начале отрезка, т.е.
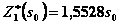 при
при 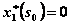 .
.
На этом условная оптимизация заканчивается. Используя ее результат и исходные данные, получим 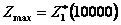 ,
, 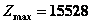 .
.
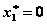 ,
, 
(все средства выделяются II отрасли) 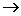
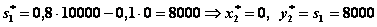
(все средства выделяются II отрасли) 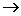
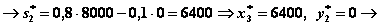
(все средства выделяются I отрасли) 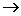
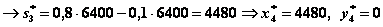
(все средства выделяются I отрасли).
Оптимальная прибыль за 4 года, полученная от двух отраслей производства при начальных средствах 10000 ед., равна 15528 ед. при условии, что I отрасль получает по годам (0; 0; 6400; 4480), а II отрасль – соответственно (10000; 8000; 0; 0).
 2014-02-02
2014-02-02 4738
4738








