Общая постановка задачи динамического программирования

Динамическое программирование (ДП) — метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Начало развития ДП относится к 50-м годам XX в. Оно связано с именем Р.Беллмана.

Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели ДП применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т. п.

В реально функционирующих больших экономических системах еженедельно требуется принимать микроэкономические решения. Модели ДП ценны тем, что позволяют на основе стандартного подхода с использованием при минимальном вмешательстве человека принимать такие решения. И если каждое взятое в отдельности такое решение малосущественно, то в совокупности эти решения могут оказать большое влияние на прибыль.

Приведем общую постановку задачи ДП. Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т. п. В результате управления система (объект управления) 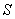переводится из начального состояния 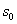в состояние 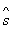. Предположим, что управление можно разбить на 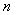шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему 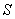из начального состояния в конечное, представляет собой совокупность 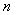пошаговых управлений.

Обозначим через 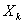управление на 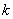-м шаге (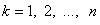). Переменные 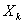удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми ( 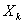может быть числом, точкой в n-мерном пространстве, качественным признаком).

Пусть 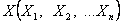— управление, переводящее систему 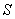из состояния 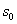в состояние 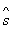. Обозначим через 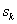состояние системы после k-го шага управления. Получаем последовательность состояний 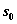, , 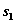…, , , 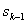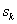…, , , 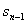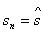которую изобразим кружками (рис. 4.5).