Лекция №5. Классификация систем. Классификационные признаки Классы Природа элементов Реальные и абстрактные Происхождение Естественные и

Классификация систем.

Классификационные признаки	Классы
Природа элементов	Реальные и абстрактные
Происхождение	Естественные и искусственные
Длительность существования	Постоянные и временные
Изменчивость свойств	Статические и динамические
Степень сложности	Простые, сложные и большие
Отношение к среде	Открытые и закрытые
Реакция на возмущающие действия	Активные и пассивные
Характер поведения	С управлением и без управления
Степень связи с внешней средой	Открытые, изолированные, закрытые, открытые равновесные, открытые диссипативные
Степень участия в реализации управляющих воздействий человека	Технические, человеко-машинные, организованные

Статические системы — такие системы, при исследовании которых изменениями можно пренебречь. Это система с одним состоянием.

Простые системы могут быть описаны известными математическими отношениями.

Сложные системы характеризуются многомерностью (большим числом составных элементов), многообразием природы элементов.

К сложной системе можно отнести систему, обладающую, по крайней мере, одним из ниже перечисленных признаков:

ñ систему можно разбить на подсистемы и изучать каждую из них отдельно

ñ система функционирует в условиях существенной неопределённости и воздействия среды на неё, обуславливает случайный характер изменения её показателей

ñ система осуществляет целенаправленный выбор своего поведения

Большие системы:

ñ большие размеры

ñ сложная иерархическая структура

ñ циркуляция в системе больших информационных, энергетических и материальных потоков

ñ высокий уровень неопределённости в описании системы

Открытые системы обмениваются с окружающей средой энергией и веществом. Изменение энтропии открытой системы: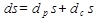

К постоянным системам относятся искусственные системы, которые в процессе заданного времени функционирования сохраняют существенные свойства, определяемые предназначением этих систем.

Реальными системами являются объекты, состоящие из материальных элементов.

Абстрактные системы — это то что не существует в реальном мире, создаются путём мысленных образов.

Параметризация и оценка качества систем.

Параметр выступает как идентификатор, имеющий определённые характеристики и используемый для количественной оценки свойств системы, а так же для различия между собой объектов некоторого множества.

Определение параметров системы означает выделение из множества переменных, характеризующих различные свойства и состояния системы, небольшого числа величин, называемых «параметрами порядка», или «параметрами организационной эффективности».

Провести параметрическое исследование системы означает:

1. определить состав её параметров, которые выступают индикаторами жизнеспособности и качества системы

2. установить критерии их оценки.

Важный аспект параметрического исследования связан с фиксированием условий:

ñ размера или общих параметров организации (производственной мощности и товарооборота, численности персонала, стоимости основных фондов)

ñ стадии жизненного цикла организации

В этой связи при параметрическом исследовании рассматриваются 3 класса параметров системы:

ñ общие параметры управления

ñ системные параметры

ñ параметры организации управления

Концептуальная модель.

Выделяют статическую и динамическую параметризацию системы

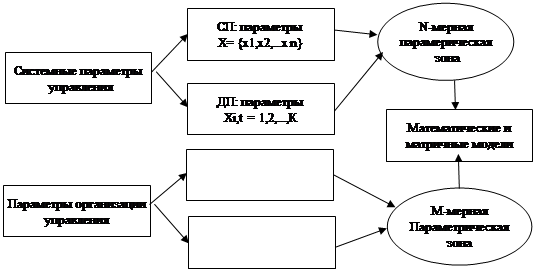статическая параметризация представляет расчет равнодействующих величин, т. е. среднеарефмитических, средневзвешенных и среднегеометрических величин параметров за К «элементарных» ti (I = 1,2,...K) периодов работы системы.

Динамическая параметризация означает расчет последовательности параметров по каждому элементарному периоду ti (I = 1,2,...K) и статистическую оценку параметров по элементарным периодам интервала времени К.

Каждая конкретная система (S) характеризуется набором свойств, под которыми понимаются величины, отображающие поведение моделируемого объекта (реальной системы) и учитываются условия её функционирования во взаимодействии с внешней средой (системой) (Е).

При построении математической модели системы (S) необходимо решить вопрос о её полноте. Полнота моделирования регулируется, в основном, выбором границ «система S – среда Е».

Математическая модель системы (S) может быть представлена в виде подмножеств:

- совокупность Х входных воздействий на (S): 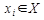i = 1,2,...

- совокупность воздействий внешней среды на (S):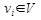i = 1,2,...

- совокупность внутренних параметров системы (S):

- совокупность выходных характеристик системы (S): 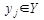j = 1, 2,....

В общем случае X, V, H, Y – множества, содержащие как детерминированные так и стохастические составляющие.

ñ Входные воздействия Х и внутренние параметры системы S являются независимыми (экзогенными) переменными.

ñ Выходные характеристики системы S являются зависимыми переменными (эндогенными).

Прогресс функционирования системы S описывается оператором :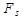

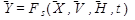
закон функционирования FS может быть функцией, функционалом, логическими условиями, алгоритмом, таблицей или словесным описанием правил.

Для статических условий математическая модель есть отображения X, V, H в Y, т. е.

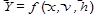
Таким образом, под математической моделью объекта понимаем конечное множество переменных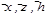вместе с математическими связями между ними и характеристиками.