2014-02-02
3279
Заключение
Исследование процессов методом теории подобия должно состоять из следующих этапов:
1) Составив дифференциальные уравнения и установив условия однозначности, проводят подобное преобразование этих уравнений и находят критерии подобия.
2) Опытным путём на моделях устанавливают конкретный вид зависимости между критериями подобия.
Обычно представляют: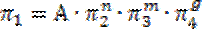 
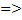т.е. в виде степенных зависимостей.
Численные показатели степеней и коэффициент А определяются экспериментально на модели.
Необходимо отметить двоякую роль критериев подобия:
1)Значения критериев обеспечивают количественный перенос результатов опыта на оригинал (численное равенство критериев);
2)На основе критериев определяют, какой должна быть модель, чтобы обеспечит условия моделирования.
Пример: течение жидкости по трубопроводу:
Форма модели 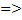определяется условиями геометрического подобия.
Размеры 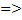определяется соображениями целесообразности (большая - дорогая, малая – зависит от погрешности).
Для подобия необходимо:
;
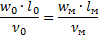
Для одной жидкости (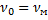
):
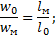
Таким образом, скорость жидкости в модели должна быть обратно пропорциональна её размеру, т.е. чем меньше модель, тем больше скорость.
Запишем уравнение Навье-Стокса для одномерного движения несжимаемой жидкости, когда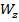 
изменяется только в направлении оси Z:
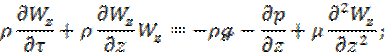
В этом уравнении левая часть учитывает действие силы инерции в правой части член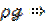 
сила тяжести, член 
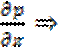силы гидростатического давления, а 
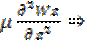силы вязкого трения.
По 
теореме
Критерии гидродинамического подобия получим путём деления каждого члена уравнения на один из других, отбрасывая при этом знаки математических операторов (плюс, минус, дифференцирования):
1.
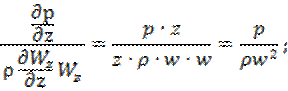
Это критерий Эйлера:
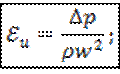
Физический смысл: выражает меру отношения силы гидростатического давления к силам инерции в подобных потоках.
Этот критерий определяемый, равенство его в подобных системах является следствием подобия.
2.
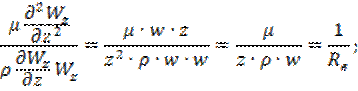
(заменить z на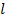 
)
Это критерий Рейнольдса:
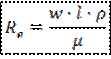
Физический смысл: выражает меру отношения инерционных и вязкостных сил в подобных потоках.
Это определяющий критерий, его равенство является необходимым условием подобия.
3.
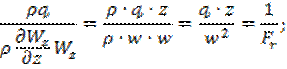
Это критерий Фруда:
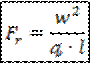
Физический смысл: выражает меру отношения инерционных и гравитационных сил (сил тяжести) в подобных потоках.
4.
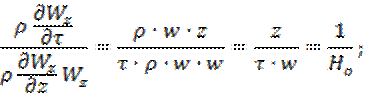
Это критерий гомохронности:
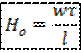
Физический смысл: выражает меру отношения локального изменения инерционных сил к конвективному, и учитывает неустановившейся характер движения в подобных потоках.
Применяется только при неустановившемся режиме; для установившихся процессов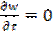 
и критерий 
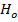выпадает.
Это определяющий критерий, неустановившиеся процессы могут быть подобны лишь в том случае, если подобные изменения всех переменных в сходственных точках будут проходить в интервалы времени, определяемые требованием: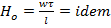 
По 
теореме
Решение уравнения Навье-Стокса можно представить в виде функциональной зависимости между полученными критериями подобия:
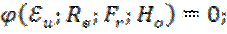
В ряде случаев эта зависимость должна быть дополнена параметрическими критериями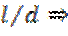 
это отношение одноименных величин (инвариант, симплекс геометрического подобия) = idem для сходных точек подобных систем.
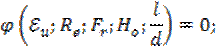
Все критерии, кроме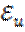 
, являются определяющими, т.к. составлены исключительно из величин, входящих в условия однозначности.
В критерий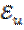 
входит величина 
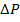, значение которой при движении по трубе полностью определяется формой и размерами 
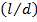, физическими свойствами жидкости 
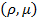и распределением скоростей на входе в трубу и её стоках (начальные и граничные условия).
По 
теореме
Следовательно, для подобия необходимо и достаточно:
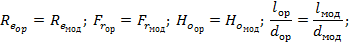
Следствием выполнения этих условий будет:
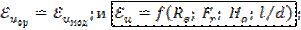
Это критериальное уравнение гидродинамики.
Из критериального уравнения определяют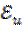 
, а из него 
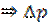– потерю напора при движении жидкости.
Зависимость представляют обычно в виде степенной:
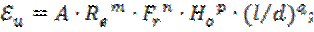
Показатели m; n;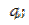
p и A определяются опытным путём.
В ряде случаев критериальное уравнение упрощается, когда процесс не зависит от какого-либо критерия, т.е. является автомодельным по нему:
1. В случае установившегося движения исключается критерий гомохронности:
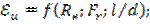
2. При установившемся видимом движении жидкости в горизонтальной трубе влияние собственного веса (силы тяжести) на перепад давления мало и можно записать:
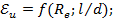
Но при истечении жидкостей критерий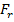 
необходимо учитывать.
Необходимо отметить, что число критериев подобия, зависимость между которыми заменяет дифференциальное уравнение, на единицу меньше членов этого уравнения (например, членов уравнения 5, число критериев
5-1=4).
К этому присоединяются параметрические критерии, число которых зависит от числа пар одноименных величин (одноименные 2
x,z; одна пара = один параметрический критерий).
