Запишем уравнение движения (3.8) с учетом внутреннего трения в следующем виде:
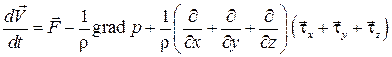 . (7.1)
. (7.1)
Напомним, что 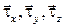 представляют собой касательные напряжения от силы трения, действующие на площадки, перпендикулярные соответствующим осям координат. Каждая из этих составляющих, в свою очередь, может быть представлена в виде суммы трех проекций на оси координат. Таким образом, мы имеем тензор напряжений (3.10), симметричный относительно главной диагонали, т. е.
представляют собой касательные напряжения от силы трения, действующие на площадки, перпендикулярные соответствующим осям координат. Каждая из этих составляющих, в свою очередь, может быть представлена в виде суммы трех проекций на оси координат. Таким образом, мы имеем тензор напряжений (3.10), симметричный относительно главной диагонали, т. е. 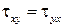 ,
, 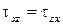 ,
, 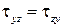 .
.
Составляющие тензора напряжений можно выразить с помощью обобщенного закона Ньютона (3.12):
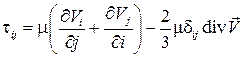 ,
,
где 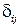 имеет вид телеграфного сигнала (или единичной матрицы), принимая значения
имеет вид телеграфного сигнала (или единичной матрицы), принимая значения 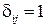 при
при 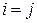 или
или 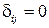 при
при 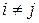 ;
; 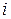 и
и 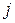 – координатные направления.
– координатные направления.
Тогда, например:
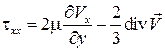 ,
, 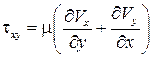 .
.
С учетом выражений (3.10) для 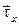 ,…, расписав каждую из составляющих
,…, расписав каждую из составляющих 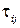 тензора напряжений, запишем уравнение движения (7.1) в проекциях на оси координат:
тензора напряжений, запишем уравнение движения (7.1) в проекциях на оси координат:
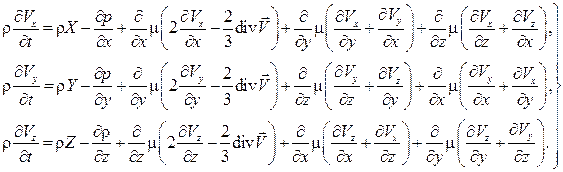 (7.2)
(7.2)
Уравнения (7.2) и есть уравнения Навье–Стокса. В общем случае коэффициент вязкости 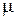 зависит от температуры. Если считать
зависит от температуры. Если считать 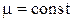 , то уравнения Навье–Стокса будут иметь вид
, то уравнения Навье–Стокса будут иметь вид
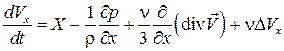 ,
,
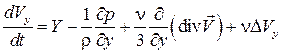 , (7.3)
, (7.3)
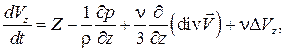
где 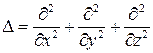 – оператор Лапласа.
– оператор Лапласа.
Точное решение задачи обтекания какого-либо тела, сводящееся к интегрированию сложных дифференциальных уравнений при заданных граничных условиях, представляет огромные трудности. Для получения каких-либо частных решений прибегают к упрощению дифференциальных уравнений.
Так Д. Стокс, решая задачу об обтекании шара потоком вязкой жидкости и сделав допущение о малости инерционных членов, отбросил их полностью. Однако такое упрощение справедливо только при очень малых числах Рейнольдса, незначительно отличающихся от единицы. О. Рейнольдс принял модель несжимаемой жидкости, отбросив полностью инерционные члены, а из вязких членов оставил главнейшие. Этот метод применяется при решении гидродинамических задач теории смазки (при малых числах 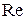 ). Другие авторы вместе с вязкими членами оставили в уравнении только важнейшие из инерционных членов, которые к тому же линеаризируются путем замены неизвестной скорости перед производной ее характерным значением. Однако и этот метод применим при небольших числах
). Другие авторы вместе с вязкими членами оставили в уравнении только важнейшие из инерционных членов, которые к тому же линеаризируются путем замены неизвестной скорости перед производной ее характерным значением. Однако и этот метод применим при небольших числах 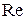 и к тому же достаточно сложен.
и к тому же достаточно сложен.
При изучении обтекания тел при больших числах Рейнольдса, характерных для авиационной и ракетной техники, применяют метод упрощения уравнений Навье–Стокса, основанный на понятии пограничного слоя.
 2015-03-22
2015-03-22 3536
3536
